Um helicóptero está voando em direção ao norte a e a uma altitude constante de . Abaixo, um carro viaja para o oeste em uma estrada a . No momento em que o helicóptero cruza a estrada, o carro está a leste dele.
(a) Com que velocidade estará mudando a distância entre o carro e o helicóptero no momento em que o helicóptero cruza a estrada?
(b) Naquele momento, a distância entre o carro e o helicóptero estará crescendo ou decrescendo?
Passo 1
Primeiro vamos visualizar o que está acontecendo (inclusive lembrar pra onde fica leste e oeste hehe):
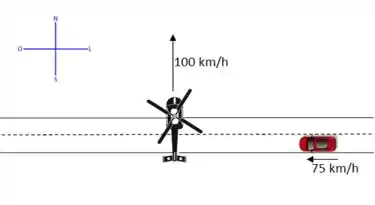
Mas pera pera pera, você tá vendo que o helicóptero está se afastando do carro no sentindo Norte-Sul, enquanto o carro se aproxima do helicóptero no sentido Leste-Oeste? Ou seja, nesse caso o movimento relativo desses dois caras é um pouco mais complicado pois está em duas direções.
Passo 2
(a)
Por facilitar, vamos colocar isso tudo no . Colocando o sentido Norte-Sul no eixo e o sentido Leste -Oeste no eixo . O helicóptero é a bolinha preta e o carro a bolinha vermelha:
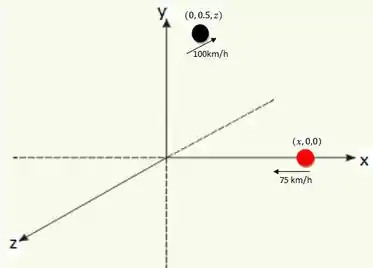
Num instante qualquer o helicóptero está em pois está a uma altura constante de . E além disso está andando na direção negativa de com aquela velocidade e não anda das direções de e . Então, para o helicóptero:
E num instante qualquer o carro está na posição e andando no sentido negativo de com aquela velocidade e não anda nas direções e . Logo, para o carro:
Passo 3
Já que estamos interessados na direção entre esses dois caras, temos que a direção entre dois pontos no é:
Aplicando nos pontos
Derivando essa expressão pra relacionarmos as taxas de variação:
Usando que derivada de constante é zero e a Regra da Cadeia:
Passo 4
Se quisermos usar nossa equação ainda vamos precisar descobrir quanto valiam , e no instante desejado.
Como o momento que nos interessa é o momento em que o helicóptero cruza a estrada e a estrada está no eixo , isso nos diz que:
E além disso o carro está a leste do helicóptero, então:
E como:
Passo 5
Substituindo tudo isso na equação (1):
(b)
Como , a distância está decrescendo.
Resposta
(a)
(b) decrescendo