Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 46

Em um relógio, o ponteiro dos minutos tem 4   c m de comprimento e o das horas, 3   c m . Com que rapidez estará variando a distância entre as extremidades do ponteiro às 9   h o r a s ?

Passo 1

Primeiro vamos ter que pensar como vamos fazer alguma equação aonde apareça essa distância entre as extremidades do ponteiro. Vem comigo:

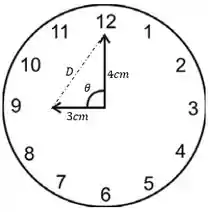
Vamos definir que num instante qualquer o ângulo entre os ponteiros é θ e a distância entre as extremidades é D . Podemos pela lei dos cossenos falar que:

D 2 = 3 2 + 4 4 - 2 3 4 cos ⁡ θ

D 2 = 25 - 24 cos ⁡ θ

Passo 2

Já que estamos interessados em com que rapidez estará variando a distância entre as extremidades, ou seja, o d D / d t , vamos derivar essa expressão em relação ao tempo:

d D 2 d t = d d t 25 - 24 cos ⁡ θ

Pelas propriedades de derivada e usando a regra da cadeia, vamos chegar em:

2 D   d D d t = ( - 24 ) ( - sin ⁡ θ ) d θ d t

2 D   d D d t = 24 sin ⁡ θ d θ d t                   e q u a ç ã o   ( 1 )

Passo 3

Agora pra usar essa equação que encontramos, precisamos descobrir quanto valia o D , o sin ⁡ θ   e o d θ / d t no instante pedido:

Quando são 9 h r s o relógio está exatamente como no desenho lá em cima, ou seja θ = 90 ° :

sin ⁡ θ = sin ⁡ 90 ° = 1

cos ⁡ θ = cos ⁡ 90 ° = 0

Para encontrarmos o valor de D , vamos usar :

D 2 = 25 - 24 cos ⁡ θ                                             ⇒ cos ⁡ θ = 0                             D 2 = 25 - 24 0

D = 5   c m

Passo 4

Pra acharmos o d θ d t vamos ter que lembrar o seguinte: o ponteiro dos minutos anda mais rápido que o das horas, mas eles andando no mesmo sentido. Então a velocidade com que o ângulo entre eles varia é velocidade com que o ponteiro dos minutos anda menos a velocidade com que o ponteiro das horas anda:

d θ d t =     v e l o c i d a d e   p o n t e i r o   m i n u t o s - ( v e l o c i d a d e   p o n t e i r o   h o r a s )

Mas o ponteiro dos minutos varre 2 π   r a d em 1 h r = 60   m i n . Então:

v e l o c i d a d e   p o n t e i r o   m i n u t o s = 2 π 60 = π 30   r a d / m i n

E o ponteiro das horas vale 2 π   r a d em 12 h r s = 720   m i n . Então:

v e l o c i d a d e   p o n t e i r o   h o r a s = 2 π 720 = π 360  

Aí chegamos que:

d θ d t = π 30 - π 360   = 11 π 360   r a d / m i n

Passo 5

Se substituirmos todos esses dados na equação (1):

2 D   d D d t = 24 sin ⁡ θ d θ d t              

2 5 d D d t = 24 1 11 π 360  

5 d D d t = 12 11 π 360    

( 5 )   d D d t = 11 π 30              

d D d t = 11 π 15 0   c m / m i n            

Resposta

11 π 150   c m / m i n            

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um avião está voando horizontalmente a uma altitude constante de 4.000p é s é acima de um ponto de observação fixo (ver figura abaixo). Em um certo instante, o ângulo de elevação θ é de 30 ° e está de
Trigo está saindo através de uma calha de escoamento a uma taxa de 10p é s 3 / m i n é e caindo em uma pilha cônica cujo raio da base é sempre a metade da altura. Com que rapidez estará aumentando a c
Grãos caem de uma calha de escoamento a uma taxa de 8m 3 / m i n , formando uma pilha cônica cuja altura é sempre o dobro de seu raio. Com que rapidez a altura da pilha estará crescendo no momento em
Um avião está voando a uma altitude constante e com uma velocidade constante de 600k m / h . Um míssil antiaéreo é disparado em uma linha reta perpendicular à trajetória de voo do avião, de tal forma
Para a câmera e o foguete da Figura 3.4.5, a que taxa estará subindo o foguete quando o ângulo de elevação for de π / 4 radianos e se estiver crescendo a uma taxa de 0,2r a d / s ?