Um holofote está a km de uma estrada reta e mantém sua luz focalizada em um automóvel que está viajando a uma velocidade escalar constante de km/h. Ache a taxa segundo a qual o feixe de luz está mudando de direção (a) quando o carro está no ponto da estrada mais perto do holofote e (b) quando o carro está a km desse ponto.
Passo 1
Esse vai ser um problema de taxas relacionadas, a primeira coisa a tentar se fazer neste tipo de questão é um esboço do que está acontecendo, olhem na imagem abaixo como facilita o entendimento.
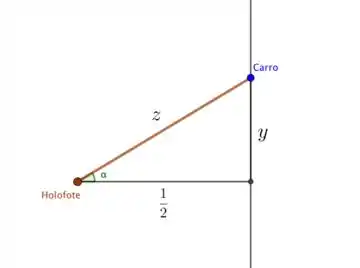
Temos a estrada reta em que o carro está, um holofote com distância de km da estrada e marquei também os comprimentos (não vamos usar o ) e . O problema quer saber a taxa segundo a qual o feixe de luz está mudando de direção, ou seja, como o ângulo está variando em relação ao tempo.
Precisamos descobrir e temos a velocidade escalar do carro, que é a taxa de variação do nosso em relação ao tempo, ou seja .
Passo 2
Vamos agora determinar uma expressão para . Aplicando tangente, temos:
E da função inversa temos que:
com .
Tá bom por enquanto.
Passo 3
Para achar precisamos derivar implicitamente a expressão de em relação ao tempo. Vamos então tomar a derivada de ambos os lados:
Agora devemos lembrar que em que é uma função. No nosso caso, .
Chegamos então em:
Passo 4
Agora vamos substituir .
Essa é a expressão que nos dá a taxa pedida.
Passo 5
- Qual a taxa quando o carro está no ponto da estrada mais perto do holofote?
Esse ponto acontece justamente quando nosso . Vejam só lá no nosso desenho. Sendo assim, quando
Daí o feixe de luz está mudando a direção em rad/h.
Passo 6
- Qual a taxa quando o carro está a km desse ponto (ponto mais perto do holofote).
Esse ponto acontece justamente quando nosso . Sendo assim, quando
Daí o feixe de luz está mudando a direção em rad/h.
Resposta
- rad/h
- rad/h