Identifique o tipo de seção cônica a qual a equação é dada e encontre os vértices e os focos:

Vamos passar todos os termos para o lado direito:

Como podemos perceber, possui sinal negativo, o que indica que a equação é de uma hipérbole.

Assim, vamos somar em ambos os lados para podermos nos aproximar da equação padrão da hipérbole:

Colocando o sinal negativo em evidência para podermos completar quadrados:

Completando quadrados:

Agora queremos encontrar os vértices e os focos. Mas o que são eles??

Bom... para respondermos isso temos que analisar a figura da hipérbole abaixo:

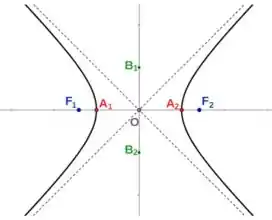
Nessa figura temos que:

• e são os focos;
• e são os vértices;
• As retas pontilhadas são as assíntotas;
• A distância do centro a um dos focos é dada por ;
• A distância do centro a um dos vértices é dada por ;
• A distância do centro a um dos conjugados é dada por .

Temos também que:

Também sabemos que a equação geral que descreve uma hipérbole centrada na origem é dada por:

Agora bora aplicar!! 😉

Como podemos perceber pela equação:

Calculamos então :

Podemos encontrar as coordenadas dos focos e dos vértices utilizando os valores de e .

Masss precisamos tomar cuidado com algumas coisinhas:

• o fato do na equação da elipse estar sendo somado a . Isso significa que há uma translação da elipse no eixo , portanto, os vértices e os focos estarão deslocados;
• também temos que, diferente da equação geral, o termo de está positivo e o de está negativo. É como se nossa hipérbole estivesse rotacionada em .

Vamos considerar isso que acabamos de mencionar para encontrar os vértices e os focos a seguir:

Pela definição dos vértices:

E pela definição dos focos: