Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 47
Trace a curva e encontre seu comprimento correto com 4 casas decimais.
Passo 1
Fala ai galerinha. De boa? Preparado para traçar uma curva parametrizada por e calcular o comprimento dessa curva?
Vamos entender um pouco como faremos isso? Se liga! 😊
Para resolver o problema
- Traçamos a curva no plano cartesiano utilizando a parametrização dada.
- Em seguida, verificamos o intervalo de integração para calcular o comprimento da curva;
- Utilizamos a fórmula do comprimento de arco para curvas parametrizadas:
- Calculamos as derivadas e e substituímos na fórmula.
- Simplificamos a expressão resultante e integramos numericamente no intervalo dado, obtendo o comprimento aproximado.
.
Agora é só resolver, Bora!
Passo 2
Primeiro vamos traçar a curva no gráfico, faremos isso escolhendo valores e substituindo nas equações de e .
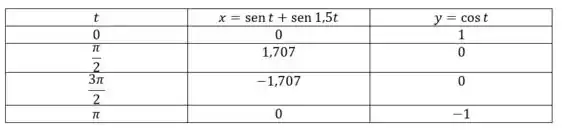
Os pontos acima podem nos ajudar a entender a curva das equações parametrizadas. No entanto podemos pedir ajuda a um software para contruir um gráfico mais completo.
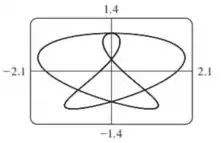
Passo 3
Observando o gráfico, podemos determinar o intervalo de que cobre uma curva completa.
Para entender isso, considere o seguinte:
- A função tem período .
- A função tem período .
- A função tem período
O período comum mais baixo entre as funções , e é , que é o mínimo múltiplo comum de e . Sendo assim o intervalode integração será.
Passo 4
Agora vamos iniciar derivando as funções em relação a .
E derivando :
Passo 5
Agora podemos substituir as derivadas na formula do comprimento do arco.
Esta integral não tem uma solução analítica simples, portanto, vamos precisar de um recurso computacional.
Passo 6
Então, no intervalo , temos que:
Prontinho, chegamos na resposta. Até a próxima! 😉