Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.Exercícios Práticos - Ex. 34
a. Identifique os valores de equilíbrio. Quais são estáveis e quais são instáveis?b. Construa uma reta de fase. Identifique os sinais de y' e y".c. Esboce uma seleção representativa de curvas integrais
Passo 1
Bem a primeira coisa a dizer é a questão completa quer também uma analise computacional. Aqui vamos nos ater apenas as soluções analíticas. Okay? Dito isso vamos em frente.
Primeira coisa que vamos analisar. Pontos de equilíbrio. Lembra que os pontos de equilíbrio são os pontos onde
Todas as nossas funções são equações diferenciais, ou seja, são funções . Então isso facilita muito a nossa vida.
Então nossa função tem raiz em e
Passo 2
Vamos construir a reta de fase. Vamos criar uma reta e botar os pontos de equilíbrio.
Show. Estamos quase acabando, falta só descobrir se é nosso ponto é estável ou instável, e para isso precisamos apenas verificar o sinal da derivada.
Passo 3
Se seguirmos essa regra
Desenha uma
Desenha uma
Vamos conseguir analisar direitinho a estabilidade dos pontos. Então vamos por seções. Pega a parte para , depois e por fim .
Para . Por exemplo , nossa derivada fica :
Para . Por exemplo , nossa derivada fica :
Para . Por exemplo , nossa derivada fica :
Isso quer dizer que nossa reta de fase fica assim :
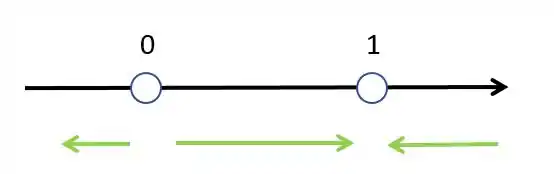
Então vamos la. Se as setas Divergem o ponto é Instável. Agora, Se as Setas Convergem para o ponto, ele é estável.
Entãoé Instável e é Estável.
Acabamos por aqui , nos vemos na próxima resolução 😊
Resposta
Pontos de Equilíbrio e
Então é Instável e é Estável.