Outra equação usada para modelar crescimento populacional é a equação de Gompertz.

Em que e são constantes positivas.

(a) Esboce o gráfico de em função de , encontre os pontos críticos e determine se cada um deles é assintoticamente eestável ou instável.

(b) Para , determine onde o gráfico de em função de é convexo e onde é côncavo.

(c) Para cada tal que , mostre que , como dado pela equação de Gompertz, nunca é menor do que , como dado pela equação logística.

Vamos primeiro usar a ideia de separação de variáveis e reescrever nossa equação logística como

Assim vamos apenas para facilitar nossa resolução fazer uma substituição. Tome , o que implica que

Assim teremos

Logo temos

Que fica um coisa bem feia

(a) Agora podemos começar a resolver nosso exercício.

Seja nossa definida por

Então nosso gráfico é dado por

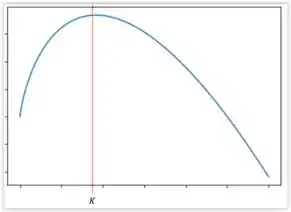
Na qual nosso ponto de equilíbrio é em . Tomando que do lado direto temos que a derivada maior que zero e do lado esquerdo uma derivada menor que zero, dizemos que nosso ponto não é nem assintoticamente estável e nem instável, ou seja, é assintoticamente semie-estável.

(b) Olhando para nossa figura no passo 3, temos que entre os intervalos , temos que

Assim temos que

O que nos da um concavidade para cima. Não há concavidade para baixo dentro deste intervalo

(c) Queremos mostrar que para todo dentro do intervalor , o valor de é maior do que o valor de , ou seja

Temos que, o gráfico de ln é dado por

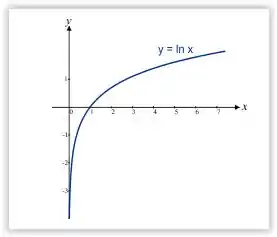
Ou seja, para valores onde , temos que

O que implica que

E finalmente temos que

Para todo tal que .