Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.8 - Ex. 37
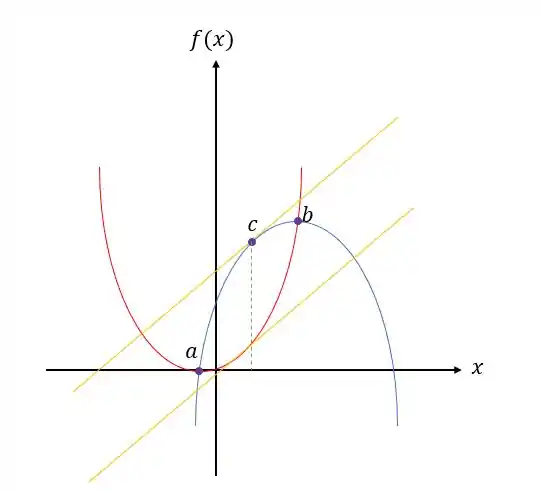
Ilustre o resultado do exercício 36 com uma figura apropriada.
Passo 1
Um exemplo disso é que precisamos de duas funções quadráticas, uma com concavidade para baixo e uma com concavidade para cima, onde vemos no ponto que e em que e no ponto nas duas concavidades é a derivada onde .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine o valor, ou valores, de c que satisfazem a equação: f b - f a b - a = f ' ( c ) Que consta da conclusão do teorema de valor médio para f x = x - 1 ,[ 1 ,3 ]
Determine o valor, ou valores, de c que satisfazem a equação: f b - f a b - a = f ' ( c ) Que consta da conclusão do teorema de valor médio para f x = x 3 - x 2 ,- 1 ,2
Para que valores de a ,meb a função: f x = 3 , x = 0 - x 2 + 3 x + a , 0x1 m x + b , 1 ≤ x ≤ 2 Satisfaz a hipótese do teorema do valor médio no intervalo[0, 2]?
Suponha f derivável em R . Prove que entre duas raízes consecutivas de f ´ há, no máximo, uma raís de f .
Prove que entre duas raízes consecutivas de uma função polinomial f existe pelo menos uma raiz de f ´ .