Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.8 - Ex. 45
Encontre uma situação física que ilustre o Teorema do Valor médio.
Passo 1
Vamos analisar o movimento de um projétil.
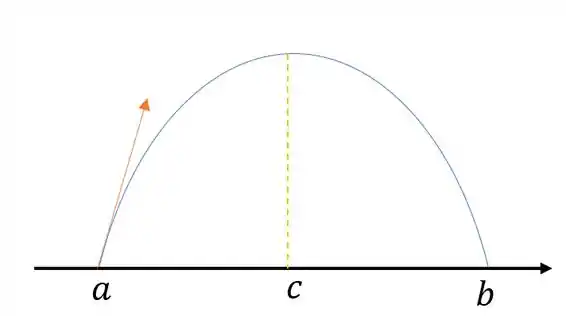
Teremos a trajetória de um corpo saindo do ponto a partir do solo em uma superfície plana, que será projetado e seguirá um caminho parabólico antes de cair novamente no chão.
Seja o ponto de projeção , e o ponto de queda. O deslocamento de altura será zero. No teorema do valor médio, podemos afirmar que deve haver um ponto , tal que:
Onde
E sendo assim:
Onde a derivada é nula e temos um ponto crítico, onde nossa função muda de concavidade.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Prove que se a 0 1 + a 1 2 + … + a n n + 1 = 0 , então a 0 + a 1 x + … + a n x n = 0 tem pelo menos uma raiz real em ] 0,1 [ .
Suponha f contínua em a , b e derivável até o 2 ª ª ordem em ] a , b [ . Sejam x 0 , x 1ex 2 ponte de a , b , com x 0x 1x 2 , e tais que f x 0 = f x 1 = f x 2 = 0 . Prove que existe pelo menos um c em
Suponha f contínua em a , b , derivável em ] a , b [ e tal que f a = f b = 0 . Suponha, ainda, que 0a . Prove que existe c em ] a , b [ tal que f ´ c = f c c . Interprete geometricamente.
Sejam feg contínuas em a , b e deriváveis em ] a , b [ , com g x ≠ 0 em a , b . Suponha ainda, que f a = g a e f b = g b . Prove que existe c em ] a , b [ tal que f ´ c g c = f c g ´ c .
Sejam ab dois reias dados. Prove que e b - e a b - ae b