Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 39
O índice de massa corporal de uma pessoa é definido por:
onde é a massa da pessoa (em quilogramas) e é a altura (em metros). Desenhe as curvas de nível , e . Uma orientação aproximada é que uma pessoa está abaixo do peso se o IMC for menor que 18,5; ideal se o IMC estiver entre 18,5 e 25; excesso de peso se o IMC estiver entre 25 e 30; e obesos se o IMC exceder 30. Sombreie a região correspondente ao IMC ideal. Alguém que pesa e tem de altura se enquadra nessa categoria?
Passo 1
Então meu amigo, vamos para mais uma resolução.
A gente tem a função de duas variáveis:
Que representa o índice de massa corporal de uma pessoa. Queremos então desenhar as curvas de nível para diferentes indicies de massa corporal.
Para desenharmos uma curva de nível de uma função de duas variáveis do tipo:
Devemos fazer:
Onde é um número real. Após colocarmos diversos valores para , teremos uma figura bidimensional em dois eixos.
Então o que faremos aqui é desenhar em um gráfico de duas dimensões a nossa função, com os valores de que nos foram passados.
Passo 2
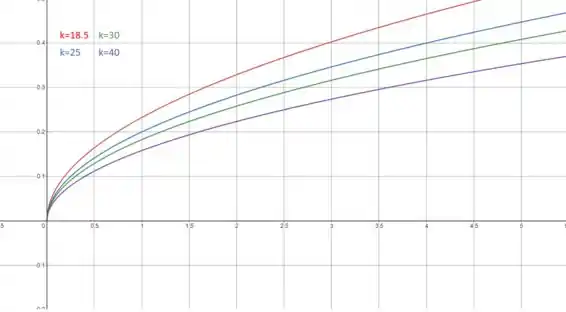
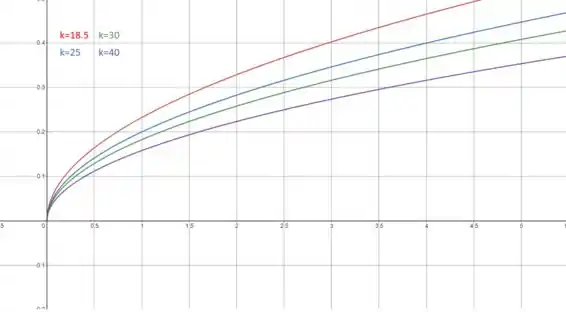
Agora, vamos considerar as curvas de nível , , e . Portanto, substituindo os valores de , temos as seguintes funções:
Agora, vamos graficar essas quatro funções em um único quadro.
Passo 3
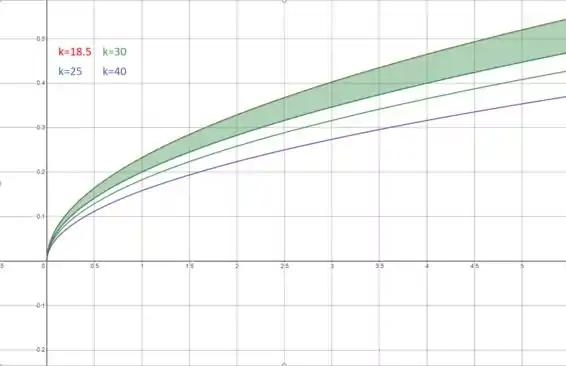
Agora, vamos sombrear a região onde o IMC é ótimo. É dado que o IMC ótimo está entre e . Portanto, o gráfico ficará assim.
Passo 4
Agora, queremos ver se uma pessoa que pesa kg e mede cm se enquadra na categoria ótima. Para isso, precisamos localizar o ponto . Portanto, temos
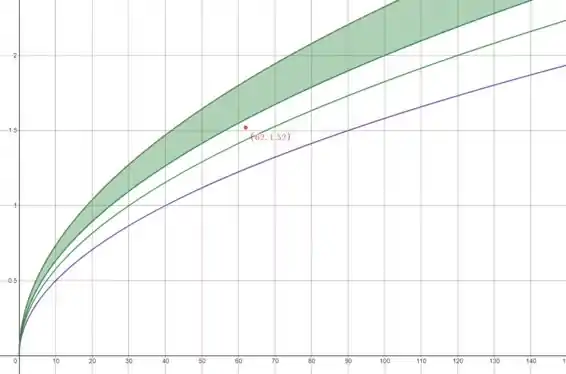
Observe que o ponto está fora da região verde. Portanto, uma pessoa que pesa kg e mede cm está fora da categoria ótima. De fato, se calcularmos o IMC da pessoa, temos:
Portanto, o IMC da pessoa está fora da categoria ótima, que é entre e
Resposta
