Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 2
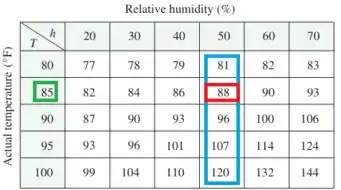
O índice (ou simplesmente Umidex) em função da unidade é a temperatura aparente do ar quando a temperatura real é e a unidade relativa é , de modo que passamos escrever . A tabela seguinte com os valores de foi extraída de uma tabela de Serviço de Administração Nacional de Oceanos e Atmosfera dos Estados Unidos.
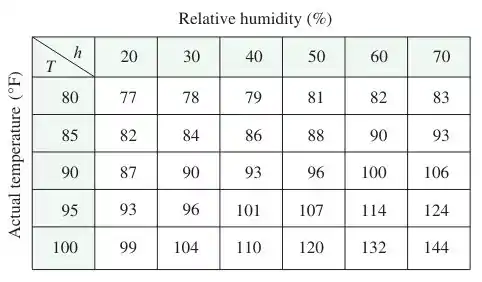
- Qual é o valor de ? Qual seu significado?
- Para que valor de temos ?
- Para qual valor de temos ?
- Qual o significado de e ?
Compare o comportamento dessas duas funções de onda de .
Passo 1
Falaeee, tudo tranquilinho??
Bom...o enunciado nos deu a seguinte tabela que relaciona a temperatura e a umidade relativa :
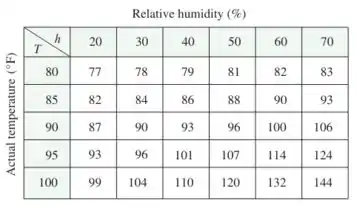
Além disso, o enunciado nos deu a seguinte função de duas variáveis:
Onde é o índice de temperatura-umidade.
Primeiramente queremos analisar quem é e explicar seu significado. Para isso, basta analisarmos os termos de e na tabela que teremos a função .
Em seguida, na letra b), queremos saber para que valor de temos . Na letra c) queremos saber para que valor temos . Para isso, basta fazermos o mesmo que na letra a).
Na letra d), assim, como na letra a), queremos explicar o significado dos valores de c) e d) encontrados.
Agora bora lá!! 😉
Passo 2
Bom... temos que:
Ou seja:
Selecionando esses valores na tabela e analisando os valores de correspondentes, encontramos:
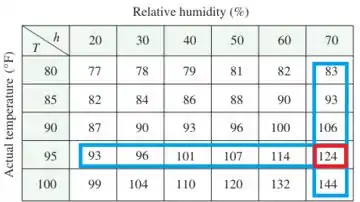
Assim, percebemos que:
Isso significa que a uma temperatura de e uma umidade relativa de o índice de temperatura-umidade é .
Passo 3
Na letra b) queremos descobrir o valor de para o qual:
Assim, selecionamos e selecionamos os valores de para :
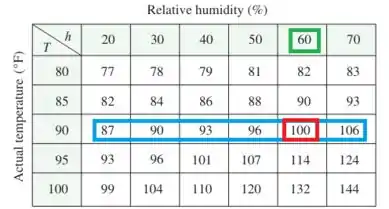
Com isso, percebemos que o único valor de é:
Passo 4
Na letra c) queremos descobrir o valor de para o qual:
Fazendo de forma análoga a letra b), temos:
Assim, temos:
Passo 5
d) significa que é fixado em e pode variar, resultando em uma função de , fornece os valores de umidade para diferentes humidades relativas quando a temperatura real é .
Da mesma forma, é uma função de uma variável que fornece os valores de umidade para diferentes humidades quando a temperatura real é .
Observando as linhas da tabela correspondentes a e , e vemos que aumenta a uma taxa relativamente constante de aproximadamente por umidade relativa, enquanto aumenta mais rapidamente (a princípio com uma taxa média de mudança por umidade relativa) e a uma taxa crescente (aproximadamente por por umidade para valores maiores de ).
Resposta
(a) .
(b) .
(c) .
(d) Comparação no passo 5.