Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 5
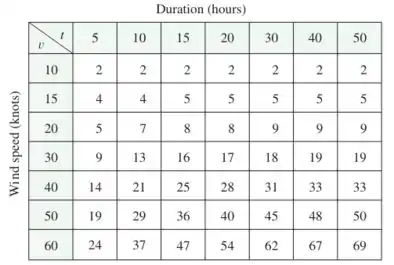
A altura das ondas em um mar aberto depende da rapidez do vento e do intervalo de tempo no qual está ventando com a mesma intensidade. Os valores da função dados em pés, são apresentados na tabela que segue.
- Qual o valor de ? Qual seu significado?
- Qual o significado da função ? Descreva seu comportamento.
- Qual o significado da função ? Descreva seu comportamento.
Passo 1
Falaeee, tudo tranquilinho??
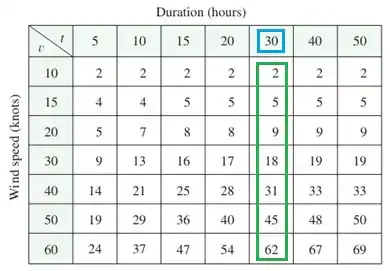
Bom...o enunciado nos deu a seguinte tabela que relaciona a rapidez do vento e o intervalo de tempo no qual está ventando com a mesma intensidade:
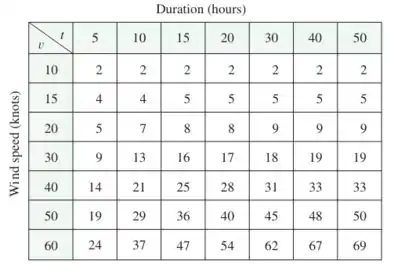
Além disso, o enunciado nos deu a seguinte função de duas variáveis:
Onde é a altura das ondas.
Primeiramente queremos analisar quem é e explicar seu significado. Para isso, basta analisarmos os termos de e na tabela que teremos a função .
Em seguida, na letra b), queremos saber o significado de . Para isso, deveremos analisar os valores de para .
E, na letra c), queremos saber o significado de . Para isso, deveremos analisar os valores de para .
Agora bora lá!! 😉
Passo 2
Bom... temos que:
Ou seja:
Selecionando esses valores na tabela e analisando o valor de correspondente, encontramos:
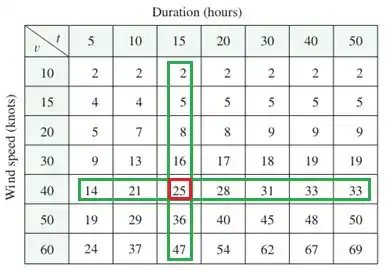
Assim, percebemos que:
Isso significa que a uma velocidade de e um tempo de , a altura é .
Passo 3
Na letra b), temos que:
Com isso, vamos analisar os valores para :
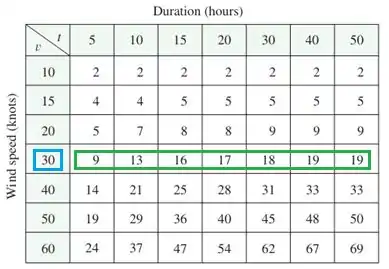
Isso significa que se fixarmos , permitimos variar , resultando na função de uma variável.
Portanto, aqui, fornece as alturas das ondas produzidas pelos ventos de soprando por horas.
Da tabela (observe a linha verde correspondente a ), a função aumenta, mas a uma taxa decrescente conforme aumenta.
De fato, os valores das funções parecem estar se aproximando de um valor limite de aproximadamente, o que sugere que os ventos de nós não podem produzir ondas superiores a cerca de .
Passo 4
Na letra c), temos que:
Com isso, vamos analisar os valores para :
Isso significa que fixamos em , novamente dando a função de uma variável.
Então, dá as alturas das ondas produzidas por ventos de velocidade soprando por .
Na tabela (veja a coluna verde correspondente a ), a função parece aumentar a uma taxa crescente, sem aparente valor limite.
Isso sugere que ventos mais rápidos ( de duração) sempre criam ondas mais altas.
Resposta
a) ;
b) fornece as alturas das ondas produzidas pelos ventos de soprando por horas;
c) dá as alturas das ondas produzidas por ventos de velocidade soprando por .