Quais das integrais a seguir, se houver alguma, serve para calcular a área da região sombreada mostrada aqui? Justifique sua resposta.
a.
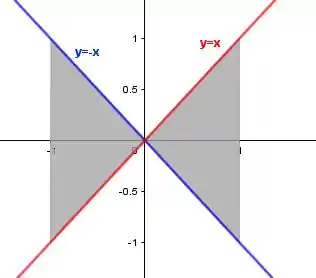
Passo 1
Lembre-se que quando calculamos a área entre regiões em relação a precismos sempre determinar qual função está “acima” e qual está abaixo. Isso é necessário para garantir que o resultado final seja positivo.
Porém, ao observarmos o gráfico vemos que eles possui duas regiões distintas, a primeira sendo de até onde está “acima” e a segunda região vai de até onde a partir de onde está “acima”.
Porém, os itens a e b só apresentam opções para calcular a integral num intervalo de até , como se ou estivesse “acima” da outra sobre todo intervalo de integração, mas vimos que isso não é verdade.
Portanto, nenhuma das opções pode calcular a área da região sombreada mostrada.
Resposta
Nenhuma das opções pode calcular a área da região sombreada mostrada.