A integral
é chamada função seno-integral, tem aplicações importantes em óptica.
- Trace o gráfico do integrando para . A função seno-integral é sempre crescente ou decresce ? Você acha que para Confira suas respostas fazendo o gráfico da função para .
Passo 1
Verificaremos, se possui raízes, ou seja, se o gráfico toca o eixo
Para isso faremos perceba que como estamos com uma divisão de polinômios, precisamos apenas igualar o numerador a zero, ou seja,
Sendo assim, são raiz para .
Passo 2
Determinaremos agora e , para em seguida verificarmos se possui máximos, mínimos ou pontos de inflexão. Dessa maneira temos que,
Pela regra do quociente,
Calculando a segunda derivada utilizando a regra quociente e a regra da cadeia,
Passo 3
Vamos agora identificar se possui pontos críticos
Se
Vamos analisar, o que acontece com os pontos críticos.
Perceba que , para valores dentro do intervalo , assume valores negativos (f é decrescente). E para valores dentro do intervalo , irá assumir valores positivos (f é crescente). Logo, é um ponto de máximo no intervalo de
Já, para valores dentro do intervalo , assume valores positivos crescente). E para valores dentro do intervalo , irá assumir valores positivos (crescente). Logo, não é um ponto de mínimo nem máximo no intervalo de
Vejamos que em assume valores positivos (f é crescente). E para valores dentro do intervalo , irá assumir valores negativos (f é decrescente). Logo, é um máximo local no intervalo
Passo 4
Para finalizar verificaremos se possui assíntotas verticais e horizontais.
No que se refere as assíntotas horizontais temos que
, pela regra do confronto (já fizemos isso )
Logo, possui uma assíntota horizontal em
No que se refere as assíntotas verticais, perceba que apesar de não estar definida em , este ponto não é uma assíntota vertical para , pois
Logo, possui assíntotas verticais em .
Resposta
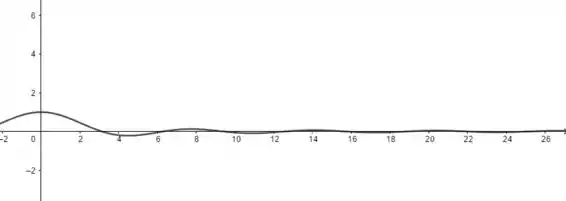
Simpara . E a função não é sempre crescente e nem sempre decrescente.