O inverso do teorema de Rolle não é válido. Dê um exemplo de uma função para a qual a conclusão do teorema de Rolle é verdadeira e para a qual (a) a condição (i) não está satisfeita, mas as condições (ii) e (iii) estão; (b) a condição (ii) não está satisfeita, mas as condições (i) e (iii) estão; (c) a condição (iii) não está satisfeita, mas as condições (i) e (ii) estão. Faça um esboço do gráfico mostrando a reta tangente horizontal em cada caso.
Passo 1
Vamos primeiro lembrar do teorema de Rolle. Seja uma função, tal que:
ela seja contínua no intervalo fechado ;
ela seja derivável no intervalo aberto ;
e .
Então existe um número no intervalo aberto , tal que .
Passo 2
- a condição (i) não está satisfeita, mas as condições (ii) e (iii) estão;
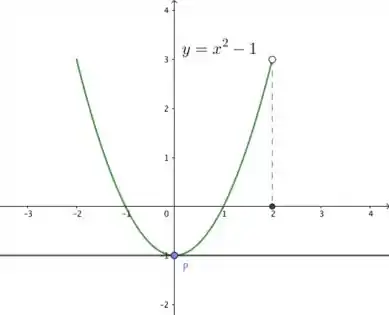
- Perceba que a função não é contínua em , ela tem um ponto de descontinuidade em (não satisfaz a hipótese).
- é derivável em .
- a condição (ii) não está satisfeita, mas as condições (i) e (iii) estão;
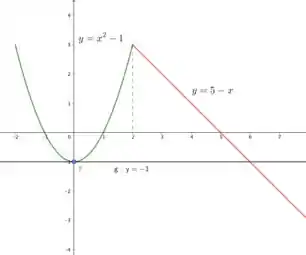
- Perceba que a função é contínua em .
- é não é derivável em , temos um bico (não satisfaz a hipótese).
- a condição (iii) não está satisfeita, mas as condições (i) e (ii) estão.
Podemos pegar a função .
Existe , tal que .
Segue o esboço da reta tangente ao gráfico de em .
Passo 3
Podemos pegar a função .
Existe , tal que .
Segue o esboço da reta tangente ao gráfico de em .
Passo 4
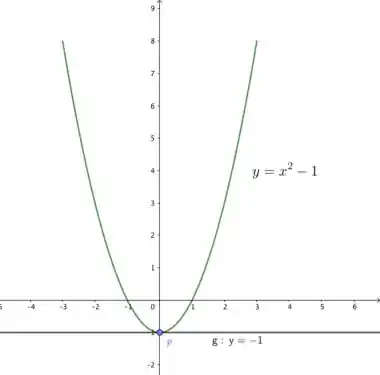
Podemos pegar a função .
- Perceba que a função é contínua em .
- é derivável em .
- (não satisfaz a hipótese).
Existe , tal que .
Segue o esboço da reta tangente ao gráfico de em .
Resposta
Ei, a resposta está no passo a passo :)