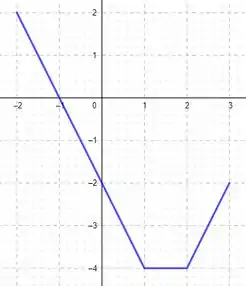
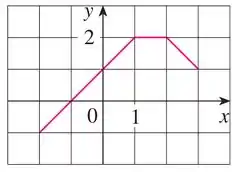
É dado do gráfico de f . Esboce os gráficos das seguintes funções:c) - 2 f x

Enunciado

Eaeee, belezinha?? Bom.. a questão nos dá o seguinte esboço de gráfico de uma função :

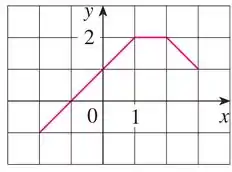
Com isso, a questão quer que esbocemos uma função que podemos chamar de que é dada da seguinte forma:

Mas como a gente faz isso??

Bom... para resolver isso a gente tem que comparar essas duas funções...

Ainda não entendeu?? Então bora junto porque não tem coisa melhor do que explicar com o próprio exemplo hehe 😉

Bom... perceba que a única diferença entre e é aquele multiplicando. Se não fosse por isso as duas funções seriam iguais.

Sabe o que esse significa??

Então, quando multiplicamos uma função por uma constante , então devemos “esticar” o gráfico em unidades verticalmente.

Em outras palavras, para o nosso gráfico, esticaríamos ele em unidades.

Mas ainda, a nossa função ainda tem um negativo junto com o , né?

Esse sinal de negativo não significa nada mais nada menos do que a inversão do nosso gráfico em relação ao eixo .

Dessa forma, esticando e invertendo o gráfico, temos:

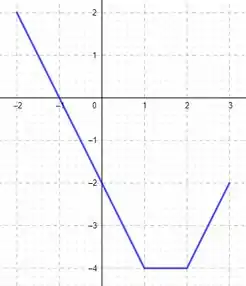
Entendeu direitinho?? Responde aee 😉