Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 47
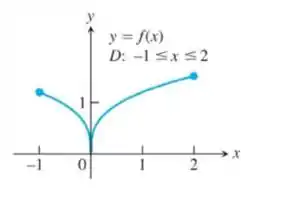
Em que pontos do domínio a função parece ser
- derivável?
- contínua, mas não derivável?
- nem contínua, nem derivável?
Passo 1
Primeiro, podemos notar que a função é definida por partes, logo, pode não ser derivável em todos os pontos.
Passo 2
Respondendo o item (a)
A função é contínua em todos os pontos do domínio e parece ser derivável em todo o domínio. Podemos notar que o ponto é comum para duas partes da função. Observando as retas tangentes, as duas tendem as ser verticais, logo, o limite para derivada pode ser o mesmo.
Item (b)
Nenhum ponto
Item (c)
Nenhum ponto
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d