Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.2 - Ex. 10
Jóse deixa Detroit às horas da tarde e guia a uma velocidade constante em direção a oeste pela rodovia . Ele passa por Ann Arbor, a milhas de Detroit, às da tarde.
- Expresse a distância percorrida em termos do tempo decorrido
- Esboce um gráfico da equação da parte
- Qual é a inclinação dessa reta? O que ela representa?
Passo 1
Fala aí!
Nessa questão, a pessoa está saindo de um ponto às horas e percorre milhas até as . Ou seja, ele levou minutos pra percorrer milha.
Na letra a, queremos a razão entre essas duas variáveis, então é só dividir uma pela outra.
Na letra b, queremos o gráfico e, pra isso, vamos usar os pontos conhecidos.
Na letra c, queremos o coeficiente angular da reta.
Lembrando que o coeficiente angular de uma reta é a sua inclinação e dada pela expressão:
Nas nossas variáveis:
Agora vamos calcular!
Passo 2
Tomando o horário de como nosso referencial, no instante de tempo , percorremos num intervalo de tempo de . Em horas .
Assim, podemos dizer que o motorista passa pelos pontos :
e
A distância percorrida em termos do tempo então é:
Passo 3
Para plotarmos esse gráfico, basta marcamos os pontos no plano cartesiano e ligar os pontos: e
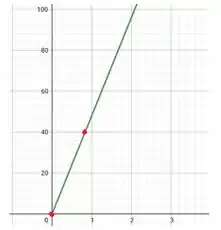
Passo 4
Pra calcular o coeficiente angular de uma reta, basta pegarmos 2 pontos dela. No caso, já temos os 2 pontos, obtidos do enunciado, aqueles lá do passo 2:
e
O coeficiente angular é a variação de dividido pela variação de :
E sendo a taxa da distância pelo tempo, ele significa a velocidade de José.
Só pra você saber, como nossa reta passa pela origem, a expressão da distância em função do tempo é:
Resposta
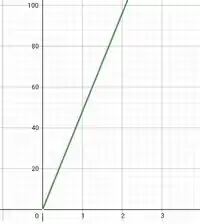
A inclinação representa a velocidade do carro e vale 48 .