Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.2 - Ex. 14
O custo mensal do uso de um carro depende do número de milhas rodadas. Lia descobriu que em maio ela gastou e guiou e, em junho, gastou e guiou milhas.
- Expresse o custo mensal como uma função da distância percorrida , supondo que a relação linear forneça um modelo apropriado.
- Use a parte para predizer o custo quando forem percorridas no mês.
- Esboce o gráfico da função. O que a inclinação representa?
- O que representa o intercepto
- Por que uma função é um modelo apropriado nessa situação?
Passo 1
Fala aí! como vai?
Nesse problema foi dada algumas informações sobre custos mensais de um carro. Em maio teve um gasto de e percorreu e em junho gastou e percorreu .
A partir daí desejamos encontrar uma “lei” de formação que relaciona o custo gasto de um carro com a quantidade de milhas rodadas pelo mesmo e estudar algumas propriedades sobre essa lei. Assim, tomemos os pontos fornecidos no enunciado para equacionarmos a nossa equação.
Com dois pontos podemos traçar uma reta, não é?
A equação da reta é dada por
Mas nesse caso, como estamos fazendo e , então
Onde é um ponto pertencente à reta e é o coeficiente angular da reta que é calculado por
Bora começar!
Passo 2
Vamos começar calculando o coeficiente angular da nossa reta utilizando
Se e
Substituindo e um dos pontos na equação da reta, chegamos em
Simplificando...
Tranquilo até aqui?
Passo 3
Com a lei de formação em mãos podemos substituir o valor de e encontraremos o custo para essa distância percorrida, fazendo
Podemos ainda plotar essa função esboçando os pontos no plano cartesiano e ligando eles através de uma reta.
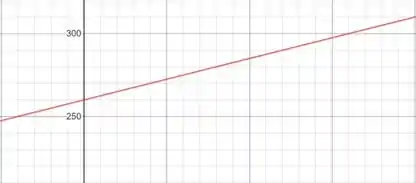
Onde a inclinação dessa reta indica um aumento no custo por milha de e o ponto onde esse gráfico intercepta o eixo representa um custo fixo de .
Além disso, percebemos que uma função linear fornece um modelo adequado nessa situação porque fixamos custos mensais como pagamentos de seguros e automóveis, por exemplo, além de custos que aumentam à medida que você dirige, como gasolina, óleo, e pneus, e o custo destes para cada milha adicional percorrida é constante.
E aí! entendeu tudo? Responde Aí!
Resposta
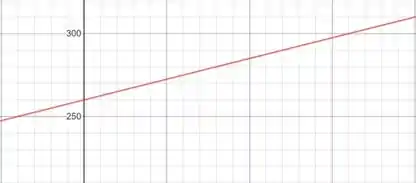
A inclinação representa um aumento no custo por milha de
o intercepto em representa o custo fixo de
Uma função linear é um modelo adequado nessa situação porque fixamos um valor de custo mensal como pagamento de seguros, por exemplo, além de custos que aumentam à medida que você dirige.