Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 44
Justifique geometricamente: e são perpendiculares se e somente se .
Passo 1
Para duas retas serem perpendiculares é necessário que o coeficiente angular de uma seja igual ao oposto do inverso do coeficiente angular da outra.
Vamos considerar que a inclinação das retas r e s são respectivamente e , conforme a figura abaixo:
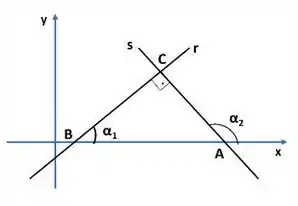
No triângulo ABC temos a relação:
Vamos calcular a tangente dos dois lados da equação:
Como a tangente de um ângulo é dada pela razão entre o seno e o cosseno deste ângulo, podemos fazer:
Passo 2
Vamos usar agora as relações da soma de arcos:
Fazendo:
e
Substituindo no que achamos da relações da soma de arcos:
Pronto, conseguimos justificar.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine se o conjunto dado é uma função. Se for, qual seu domínio? x ,y x = y + 1 3 - 2
Determine se o conjunto dado é uma função. Se for, qual seu domínio? x ,y x = y 2
Determine se o conjunto dado é uma função. Se for, qual seu domínio? x ,y y = x - 1 2 + 2
Determine se o conjunto dado é uma função. Se for, qual seu domínio? x ,y y = x 2 - 4
Determine se o conjunto dado é uma função. Se for, qual seu domínio? x ,y x = y 3