Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 28f
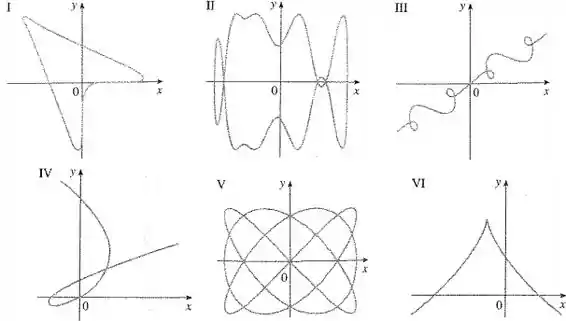
Ligue as equações paramétricas aos gráfico de I-VI.
Passo 1
A questão fornece uma curva parametrizada e pede para identificarmos o seu gráfico.
Nesse caso,
Para resolvermos essa questão sem de fato plotarmos o gráfico da curva paramétrica, apenas analisando a equação, nós deveremos analisar pontos importantes da função. Deveremos analisar interseção com os eixos, deveremos analisar o que ocorre quando , deveremos analisar periodicidade da nossa função.
Passo 2
Como tanto como são funções trigonométricas, a curva será limitada!
Vamos procurar interseções com eixos. Fazendo :
Assim, a curva corta o eixo em dois pontos!
Analogamente, fazemos :
Uma das formas de resolver essa equação é
Assim, uma das soluções dessa equação é .
Nesse caso
Esse é o maior valore que pode assumir: ponto extremo direito da curva!
A única curva fechada que corta o eixo em dois pontos e que corta o eixo no ponto extremo direito é mostrada no gráfico II.
Resposta
II