Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.6 - Ex. 34

Encontre o limite:

lim x → ∞ ⁡ t g - 1 x 2 - x 4

Passo 1

Eaee, belezinha?? Bom... queremos calcular o seguinte limite:

lim x → ∞ ⁡ t g - 1 x 2 - x 4

Para resolver isso precisamos fazer algumas manipulações algébricas pois se apenas substituíssemos o limite, teríamos a seguinte indeterminação:

t g - 1 ∞ 2 - ∞ 4

Também precisaremos analisar a tangente no círculo trigonométrico:

Agora bora lá!! 😉

Passo 2

Para iniciarmos a resolução do exercício, faremos uma brincadeira algébrica e deixaremos x 2 em evidência.

Assim, ficamos com:

lim x → ∞ ⁡ t g - 1 x 2 - x 4 = lim x → ∞ ⁡ t g - 1 [ x 2 1 - x 2 ]

Agora, faremos uma substituição, para isso iremos fazer uma mudança de variáveis, chamaremos esta nova variável de ϵ , então:

ϵ = x 2 ( 1 - x 2 )

Passo 3

Para continuar a resolver o exercício, precisamos saber para onde tende ϵ quando x → ∞ , para isso sabemos que:

x → ∞

Então, também podemos inferir que x 2 continuaria tendendo a infinito, ou seja:

x 2 → ∞

Logo,

1 - x 2 → - ∞

Repare que o sinal negativo aparece pois temos - x 2 , então deve aparecer - ∞ .

Daí, temos que:

x 2 1 - x 2 → - ∞

É possível enxergar este resultado pois se analisarmos que x 2 = ∞ e ( 1 - x 2 ) = - ∞ ficamos com ∞ - ∞ = - ∞ .

Então sabemos que esta nova variável ϵ esta tendendo para - ∞ ( ϵ → - ∞ ).

Passo 4

Vamos analisar o que acontece com o arco tangente quando ϵ → - ∞ :

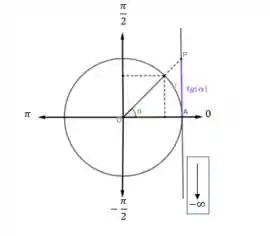
Perceba que quanto mais a tangente vai para o infinito negativo, mais ela se aproxima do ângulo - π 2 .

Assim, podemos inferir que:

lim x → ∞ ⁡ t g - 1 x 2 - x 4 = lim ϵ → - ∞ ⁡ t g - 1 ϵ = - π 2

Resposta

lim x → ∞ ⁡ t g - 1 x 2 - x 4 = - π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove que o teorema 2.4 . 5 : i Se lim x → a ⁡ f x = + ∞ e lim x → a ⁡ g x = c , onde c é uma constante qualquer então lim x → a ⁡ f x + g x = + ∞ i i Se lim x → a ⁡ f x = - ∞ e lim x → a ⁡ g x = c ,
Prove que o teorema 2.4 . 6 :Se lim x → a ⁡ f x = + ∞ e lim x → a ⁡ g x = c , onde c é uma constante não-nula, então i se c0 , lim x → a ⁡ f x ∙ g x = + ∞ i i se c0 , lim x → a ⁡ f x ∙ g x = - ∞
Prove que o teorema 2.4 . 4 i i i :Se a for um número real qualquer e se lim x → a ⁡ f x = 0 e lim x → a ⁡ g x = c , onde c é uma constante não nula, entãoSe c0 e se f x → 0 por valores positivos de f
Prove que o teorema 2.4 . 6 :Se lim x → a ⁡ f x = - ∞ e lim x → a ⁡ g x = c , onde c é uma constante não-nula, então i se c0 , lim x → a ⁡ f x ∙ g x = - ∞ i i se c0 , lim x → a ⁡ f x ∙ g x = + ∞
Prove que o teorema 2.4 . 3 i i :Se r for um inteiro positivo qualquer, então lim x → 0 - ⁡ 1 x r = - ∞ s e rf o rí m p a r + ∞ s e rf o rp a r í