Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 10
Se , deve existir? Em caso afirmativo, deve ser ? Podemos concluir algo sobre ? Explique.
Passo 1
Quando estamos falando da de um limite, precisamos ver se os valores da função próximos do ponto são iguais tanto pela esquerda do ponto quanto pela direita.
Importante: Olha que lá em cima eu não falei nada sobre o valor da função no ponto! Só nos pontos vizinhos.
Passo 2
Então, dizer que significa que em a função assume , mas nada se pode afirmar sobre os valores próximos a . Então o limite pode ou não existir.
Passo 3
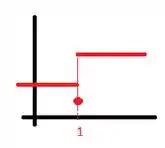
Só pra fechar com nota 10! Estou trazendo o exemplo de uma função em que e o limite em não existe.
Resposta
Nada se pode afirmar sobre o valor do limite.
Exercícios de Livros Relacionados
31-36. Use a Definição 1.4.1 para provar que o limite dado está correto. Em casa caso, para mostrar que lim x → a f x = L , fatore f x - L como: f x - L = " a l g u m ac o i s a " . x - a E, então,
Seja: f x = 0 , c o mxr a c i o n a l 1 , c o mxi r r a c i o n a l Use a definição 1.4.1 para provar que não existe lim x → 0 f x . [Sugestão: Suponha que lim x → 0 f x = L e aplique a Definição
39. b) Encontre o menor número positivo N , tal que, para cada ponto x no intervalo N ,+ ∞ , o valor da função f x = x x + 1 não esteja mais longe do que 0,01 unidade de L = 1 .
40. Em cada parte, encontre o menor número positivo N , tal que para cada ponto x no intervalo N ,+ ∞ , a função f x = 1 x 3 não esteja mais longe do que ε unidades do número L = 0 .a) ϵ = 0,1
40. Em cada parte, encontre o menor número positivo N , tal que para cada ponto x no intervalo N ,+ ∞ , a função f x = 1 x 3 não esteja mais longe do que ε unidades do número L = 0 .b) ϵ = 0,01