Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.6 - Ex. 67
Para o limite
Ilustre a definição 8, encontrando os valores de N correspondentes a
Passo 1
Bom galerinha, essa questão pede basicamente para ilustrarmos como a definação 8 se aplica a esse limite que tende ao infinito negativo.
De acordo, com a definição, temos que:
Quando um limite que tende ao infinito resulta em um valor real :
Então para todo , existe um corresponde número tal que para qualquer menor que , a distância da função para é menor que , isso é:
Quando
Temos que
Graficamente, isso pode ser representado da seguinte forma:
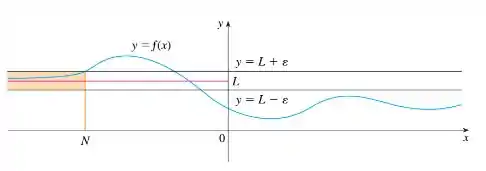
Passo 2
Usando o primeiro valor de () podemos escrever
Se
Então
Substituindo nossa função e o resultado do nosso limite, temos:
Então, nós esboçamos o gráfico de para encontrar o valor de , , e também esboçamos uma reta para ser (reta roxa) e outra para ser (reta verde)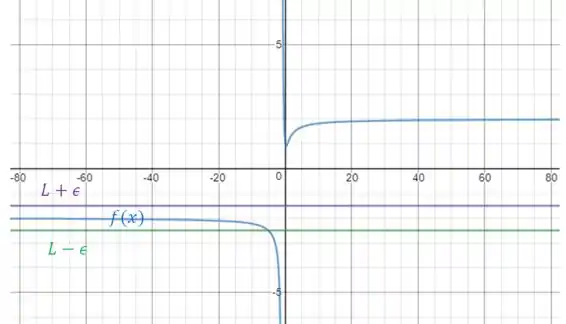 
E dando um zoom
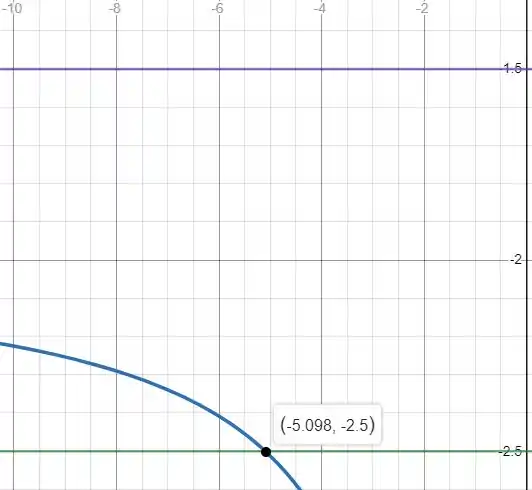
Portanto, vemos que para a função estar entre as retas é necessário que
Logo, é aproximadamente,
Passo 3
Agora, analogamente para
Podemos escrever
Se , então
Então, nós esboçamos o gráfico de para encontrar o valor de , daí ficamos com (a reta verde representa e a reta roxa representa )
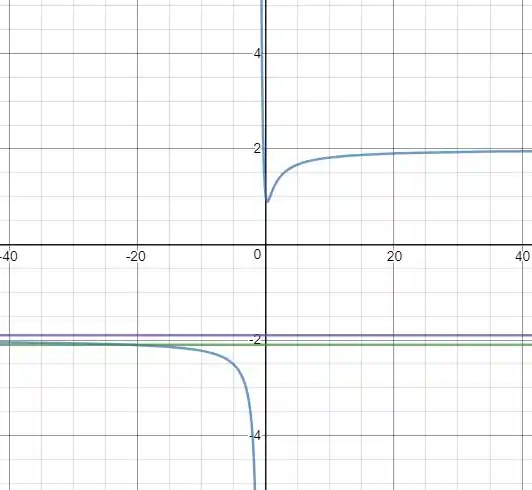
E dando um zoom
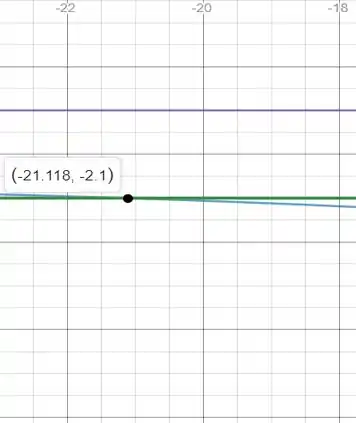
Portanto, para a função estar entre as retas é necessário que
Logo,