Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.11 - Ex. 51
Uma linha de telefone é pendurada entre dois postes separados m, na forma da catenária , em que e são medidas em metros.
- Encontre a inclinação dessa curva onde ela encontra o poste à direita.
- Encontre o ângulo entre a reta tangente e o poste.
Passo 1
Fala aí! tudo certinho?
Nesse problema temos uma linha de telefone que está disposta formando a função
Entre dois postes de entre eles como visto na figura
A partir daí queremos descobrir qual é a inclinação da reta tangente à linha no poste da direita e o ângulo entre a reta tangente da linha e o poste.
Tem ideia de como fazemos isso?
Para encontrar a inclinação da reta tangente à linha no poste da direita é relativamente simples...
A inclinação da reta tangente à uma função em um determinado ponto pode ser interpretado como a derivada da função aplicada naquele ponto, então para responder o primeiro item, basta derivarmos a função e aplicar o ponto como vemos no desenho.
Já para descobrir o ângulo , podemos fazer uma linearização da reta tangente e obter um triangulo retângulo formado pela reta tangente, o poste e o chão...
Bora começar!
Passo 2
Vamos começar derivando a função ...
Vamos usar inicialmente a regra da subtração:
Vamos derivar os termos separadamente.
Para derivar o primeiro termo vamos usar algumas regras, a fórmula da derivada de funções hiperbólicas inversas, da multiplicação por constante, do polinômio e da cadeia:
Vamos aplicar as regras então:
Sabemos que a derivada de uma constante é , logo...
Tranquilo até aqui?
Passo 3
Como é pedido a inclinação dessa curva onde ela encontra o poste à direita, isso se enconta em , assim vamos substituir esse valor na derivada que acabamos de achar:
Para calcular devemos usar a expressão abaixo:
Vamos lá então:
Show?
Passo 4
Agora para obter o ângulo , podemos encontrar a equação da reta tangente à linha e assim formar um triangulo...
A equação da reta é dada por
já temos e é , já temos e é , agora precisamos descobrir ...
Se
Então em , temos
Assim, a equação da reta tangente é dada por
Quando , vamos obter
Assim, temos duas medidas do nosso triângulo
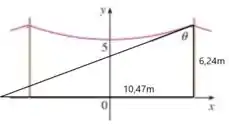
Sabemos que pela relação da tangente, temos
Ou seja
E aí! o que achou? Responde Aí!
Resposta