Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 58
58. Qual é a menor área de um triângulo que é cortado pelo primeiro quadrante e cuja hipotenusa é tangente à parábola em algum ponto
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão pede pra gente determinar qual é a menor área de um triângulo que é cortado pelo primeiro quadrante e cuja hipotenusa é tangente à parábola em algum ponto
A ideia aqui inicialmente é nós entendermos que triângulo é esse. Então, vamos começar desenhando essa figura com todas as características dadas no enunciado.
Depois temos que pensar no que faz um triângulo ter a menor área possível, lembrando que ele precisa ter um ponto de tangência com a parábola .
Ou seja, precisamos determinar uma expressão para essa área e depois minimizar essa expressão usando a derivada para encontrar seus pontos críticos.
Depois basta recalcular a área usando esses pontos.
Vem que te mostro tudinho no passo a passo.
Passo 2
Vamos começar esboçando o gráfico da curva e delimitando o triângulo que estamos querendo no primeiro quadrante.
Assim, teremos:
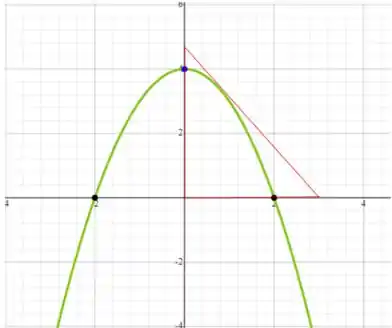
Agora vamos procurar uma expressão para o cálculo da área desse triângulo.
Passo 3
Podemos usar um ponto da curva que seja tangente à hipotenusa de nosso triângulo.
Como esse ponto pertence a curva , podemos escrevê-lo da seguinte maneira:
Para traçarmos uma reta tangente a esse ponto precisamos achar seu coeficiente angular. E a reta tangente é dada pela relação:
Como a reta é tangente a curva, o coeficiente angular da reta será a derivada da curva calculada no ponto. Sendo
Sua derivada será:
Para o ponto :
Então a reta fica o seguinte:
Que reescrevendo se torna:
Maravilha.
Passo 4
Agora vamos procurar os pontos de interseção como os eixos e para fazer o cálculo da área do triângulo.
O ponto de interseção com o eixo é
e com o eixo acontece quando Assim,
Logo,
Como a área e dada por:
Ou melhor:
Substituindo o que já encontramos, ficamos com:
Isto é,
Passo 5
Agora que já temos uma expressão para a área, vamos derivar e igualar a 0 para achar os pontos de máximo e mínimo:
Sendo:
Sua derivada será calculada uma do a regra do quociente, já que temos a divisão entre duas funções. Lembrando que
Se:
Então:
E nossa derivada da área será:
E fazendo a distributiva e reduzindo os termos semelhantes, ficamos com:
Agora igualando a zero, teremos:
Como o denominador nunca pode ser igual a zero, podemos fazer:
Resolvendo a equação do segundo grau em :
Portanto,
Como :
Perfeito.
Passo 6
Agora é só achar a área. Lembrando que:
E para
Então,
E essa é a área do menor triângulo que atende às condições do enunciado.