Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 1
Marque os pontos cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com e o outro com :
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade aqui.
A gente vai pegar esses pontos polares, e iremos marcar eles no gráfico polar. Temos um par ordenado onde:
é a distância da origem até o ponto, e é o ângulo que fazemos com a horizontal. Veja que as coordenadas:
E
Representam o mesmo ponto. Já as coordenadas:
Representam o mesmo ponto que:
Com essa informação em mãos, iremos conseguir representar o que queremos.
Passo 2
- Vamos lá, marcando o primeiro ponto:
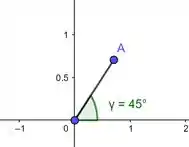
Tá aí o ponto . Quer dizer, raio 1 e ângulo
Agora pra fazer as coordenadas correspondentes a gente faz:
- o seno e o cosseno têm que ser positivos nesse caso, então a gente pode manter o e somar no ângulo. Aí a gente encontra:
- : Agora o seno e o cosseno vão ser negativos, então nosso ponto pode ser da forma: , no nosso caso:
Passo 3
Pro item b) agora, temos:
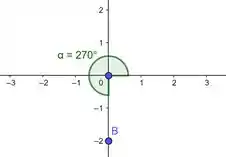
Pro raio positivo a gente pode pegar o correspondente do ângulo de forma que o raio fique positivo:
Pro raio negativo a gente pode pegar esse ângulo somado a uma volta de :
Passo 4
No item agora:
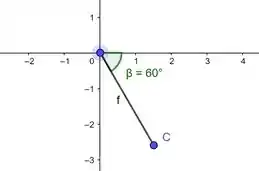
Bom, pro raio positivo, a gente pega o correspondente do primeiro quadrante:
E pro raio negativo a gente pega o oposto. Inverte o sinal do raio e pega o ângulo correspondente:
Prontinho!