Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 5.3 - Ex. 2

Uma massa de 1 kg é atada a uma mola cuja constante vale 5 N/m. A massa é solta 1 cm abaixo da posição de equilíbrio com uma velocidade de 5 cm/s para baixo. O movimento subsequente tem lugar em um meio que oferece uma força de amortecimento numericamente igual a duas vezes a velocidade instantânea.

(a) Encontre a equação de movimento se a massa sofre a ação de uma força externa igual a f t = 12 . cos ⁡ 2 t + 3 s e n ( 2 t ) .

(b) Esboce os gráficos das soluções transiente e estacionária no mesmo eixo coordenado.

(c) Esboce o gráfico da equação de movimento

Passo 1

Bora lá meu colega

(a) Vamos montar o nosso PVO

Seguindo a equação (2) do seu livro:

d 2 x d t 2 + β m d x d t + k m x = f t m

No nosso caso, temos β = 2 , m = 1 k g , k = 5   N / m e f t = 12 . cos ⁡ 2 t + 3 s e n ( 2 t ) , então:

d 2 x d t 2 + 2 d x d t + 5 x = 12 . cos ⁡ 2 t + 3 s e n ( 2 t )

E aí ele fala que “A massa é solta 1 cm abaixo da posição de equilíbrio com uma velocidade de 5 cm/s para baixo”

Então

x 0 = - 1

x ' 0 = 5

Agora temos que resolver esse PVI, fechou?

Passo 2

Temos

d 2 x d t 2 + 2 d x d t + 5 x = 12 . cos ⁡ 2 t + 3 s e n ( 2 t )

x 0 = - 1

x ' 0 = 5

Daí, temos

x c = e - t . cos ⁡ 2 t + 3 . s e n ( 2 t )

E

x p = 3 . s e n ( 2 t )

Portanto:

x t = e - t . cos ⁡ 2 t + 3 . s e n ( 2 t )

E encontramos nossa equação do movimento :D

Passo 3

(b) Agora vamos encontrar o gráfico no estado estacionário e transiente

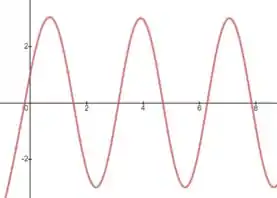
Para x c = e - t . cos ⁡ 2 t + 3 . s e n ( 2 t )

Temos uma senoide de período π e amplitude 3:

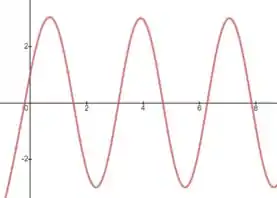
E para:

x p = 3 . s e n ( 2 t )

Temos:

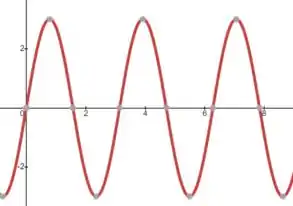
Passo 4

(c) Por fim, vamos fazer o gráfico de x c + x p :

x t = e - t . cos ⁡ 2 t + 3 . s e n ( 2 t )

Resposta

a )   x t = e - t . cos ⁡ 2 t + 3 . s e n ( 2 t )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 3-6, as figuras dadas representam o gráfico de uma equação de movimento para uma massa em uma mola. O sistema massa-mola é amortecido. Use o gráfico para determinar:(a) se o deslocamento
Uma massa de 1 kg é atada a uma mola cuja constante de elasticidade é 16 N/m e o sistema inteiro é então submerso em um liquido que oferece uma força de amortecimento numericamente igual a 10 vezes a
Um peso de 125 g é atado a uma mola de constante elástica igual a 2N / m . O meio oferece uma resistência ao movimento do peso numericamente igual à velocidade instantânea. Se o peso parte de um ponto
Uma mola de 4 cm de comprimento passa a medir 8 cm após um peso de 0,5 kg ser atado a ela. O meio no qual o peso se move oferece uma resistência numericamente igual a 2 vezes a velocidade instantânea.
Nas partes (a) e (b) do problema 9, verifique se o peso passa pela posição de equilíbrio. Em cada caso, calcule o instante no qual o peso atinge seu deslocamento extremo em relação à posição de equilí