Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 54
Seja , .
a) Esboce o gráfico de .
b) Calcule cada limite, se existir
(i)
(ii)
(iii)
(iv)
c) Para quais valores de existe ?
Passo 1
Fala aí, pessoal! Nesse problema foi dada a função
Primeiro queremos esboçar o gráfico de . E até aí é tranquilo porque o gráfico da função cosseno já é muito conhecido ne (se você não lembra, a partir de agora guarda ele na manga).
Depois precisamos determinar os limites de para tendendo a , , e . E pra isso precisamos lembrar do conceito de limites laterais. Esses sinais de + e – nos ângulos indicam se estamos nos aproximando de pela direita ou pela esquerda e isso pode fazer algumas diferencinhas.
Para obter os limites, temos que calcular os valores que a função assume quando se aproxima do valor que estamos procurando.
No fim, a questão pede os valores de pros quais existe . E agora que você lembrou dos limites laterais, eu te adianto: pra um limite existir num ponto, precisamos que os limites laterais naquele ponto sejam iguais.
Então vamos calcular limites!
Veja só! 😉
Passo 2
Vamos esboçar o gráfico de
Caso você não lembre da cara dele, é só ir atribuindo valores de dentro do intervalo e achando seus valores.
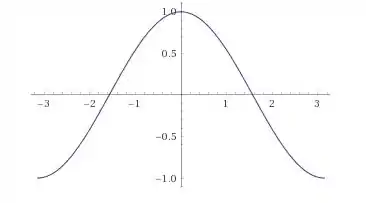
Tranquilo até aqui? 😁
Passo 3
Agora vamos pro item b!
(i) Nesse caso é só substituir o valor de na expressão:
Passo 4
(ii) Vamos calcular o limte
Vamos substituir o valor de na expressão:
No entanto, vale lembrar que estamos nos aproximando pela esquerda, ou seja, por valores próximos de mas um pouquinho menores. Então o cosseno é quase zero, mas um pouquinho maior, então é positivo.
É o contrário do que vai acontecer no próximo item.
Passo 5
(iii) Vamos calcular
Aqui estamos nos aproximando de pela direita, ou seja, por valores um pouquinho maiores que . Então o cosseno vai assumir valores um pouquinho menores que zero, ou seja, negativos:
Passo 6
E por ultimo (iv) vamos calcular
Quando os limites laterais de uma função em um ponto são iguais, então o limite geral da função no ponto existe e é igual aos limites laterais.
Como vimos nos passos anteriores que:
Podemos dizer que o limite:
Estamos quase lá! 😉
Passo 7
Agora queremos os valores de pros quais existe .
Bom já vimos que pro limite existir, os limites laterais precisam ser iguais. E como a função é contínua (isso a gente vê claramente no gráfico), o limite existe pra todo o domínio.
Para o limite
existir, pode assumir qualquer valor, dentro do intervalo especificado, ou seja
E aí! o que achou? Responde Aí! 😬
Resposta
(a)
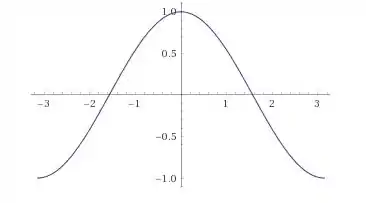
(b) (i)
(ii)
(iii)
(iv)
(c) existir, pode assumir qualquer valor entre e .