Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 17.3 - Ex. 4
4- Uma mola com uma massa de tem uma constante de amortecimento 30, e a constante da mola é 123
- Determine a posição da massa no instante se ele começar em uma posição de equilíbrio com uma velocidade de
- Faça o gráfico da função posição da massa.
Passo 1
A equação diferencial de posição da massa será então:
Para determinarmos a equação de posição em relação a nós precisaremos resolver essa e para isso precisaremos saber as raízes da equação auxiliar abaixo.
Por Bháskara temos:
Raízes complexas com e
A equação de solução para essa é igual a:
Logo:
Passo 2
- Como ele começa na posição de equilíbrio então e como sua velocidade inicial é de então
- Gráfico de :
Logo se substituirmos o ponto na equação nós teremos:
Agora fazendo a derivada em de nós teremos pela regra do produto:
Aplicando e temos:
Dessa forma a equação de movimento dessa massa será:
Passo 3
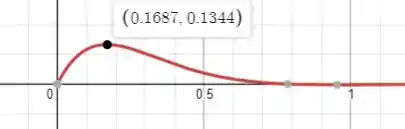
Não tem tempo negativo ok?
Resposta
Exercícios de Livros Relacionados
Encontre a solução geral da equação diferencial dada.
Em cada um dos problemas de 1 a 14, encontre a solução geral da equação diferencial dada. y ' ' + y ' = 3 sen 2 t + t cos 2 t
Em cada um dos problemas de 21 a 28:Determine uma forma adequada para Y(t) para usar o método dos coeficientes indeterminados. Use um sistema de álgebra computacional para encontrar uma solução partic
Em cada um dos Problemas de 36 a 39, use o método do Problema 35 para resolver a equação diferencial dada. y ' ' - 3 y ' - 4 y = 3 e 2 t
Determine a solução geral de y ' ' + λ 2 y = ∑ m = 1 N a m sen m π t em que λ0 e λ≠m π para m=1 ,... ,N .