Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 1
Considere o seguinte problema: encontre dois números cuja soma seja 23 e cujo produto seja máximo.
- Faça uma tabela de valores, como mostrada a seguir, tal que a soma dos números nas duas primeiras colunas seja sempre 23. Com base na evidência mostrada em sua tabela, estime a resposta para o problema
- Use o calculo para resolver o problema e compare com sua resposta da parte (a)
Passo 1
Olá, meu querido. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui temos uma aplicação de derivadas em uma situação dada.
Queremos encontrar dois números cuja soma seja 23 e cujo produto seja máximo.
Primeiro, não vamos usar o cálculo, vamos na verdade montar uma tabela e ir tentando encontrar números que somem 23 e cujo produto seja o máximo possível.
Depois, aí sim vamos usar o cálculo. Para isso, precisamos encontrar uma função a qual queremos maximizar. Para encontrar o máximo dessa função, basta derivarmos e igualarmos a zero.
E como aqui nós só trabalhamos com uma única variável, caso tenhamos mais de uma variável (nesse caso, temos dois números que queremos encontrar) vamos usar uma equação de restrição para ter uma única variável.
Passo 2
Fazendo a tabela, temos
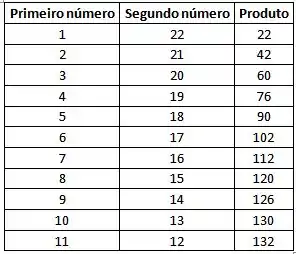
Temos que a resposta são os números 11 e 12.
Talvez e por serem exatamente a metade de sejam os melhores números, mas como na tabela nós estavámos colocando apenas números inteiros, vamos manter assim.
Passo 3
Agora usando o cálculo
Queremos maximizar o produto entre dois números, então essa é a nossa função:
No entanto, ela depende de duas variáveis. Para que ela dependa de uma variável apenas, vamos usar uma equação de restrição. Nesse caso, esses dois números quando somados precisa igualar . Portanto,
Jogando isso na função produto, temos:
Passo 4
Agora, para encontrar o máximo de derivamos e igualamos a zero, dai
Calculando
E o valor de P
Temos que os números que a soma é 23 e o produto é máximo são 11,5 e 11,5.
Resposta
- 11 e 12
- 11,5 e 11,5