É mostrado um campo de direções para a equação diferencial .
- Esboce os gráficos das soluções que satisfazem as condições iniciais dadas.
- Ache todas as soluções de equilíbrio.
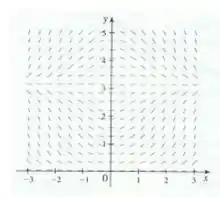
Passo 1
- (i) Nessa questão, queremos desenhar o gráfico de uma solução que pertença acampo de direções para a equação e satisfaça , que é exatamente aqui!
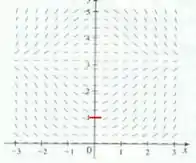
- (ii) Da mesma forma que no item (a), precisamos desenhar o gráfico de uma solução que pertença ao campo de direções para a equação e satisfaça . Assim,
Bom, como já temos o campo direcional, basta traçar um gráfico que siga a orientação das linhas de campo e obedeça , dessa forma:
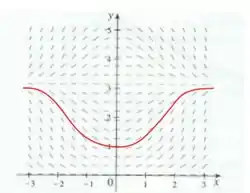
Passo 2
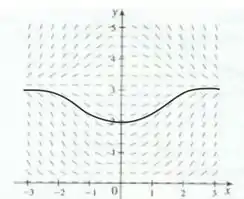
Passo 2
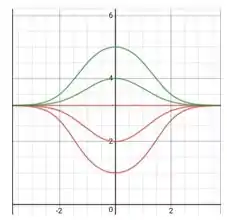
Bom, ao olharmos para esses itens percebemos que o procedimento é sempre o mesmo dos itens anteriores, então já vamos desenhar os 5 gráficos em uma imagem só para vermos todas juntas:
Passo 3
- Queremos encontrar todas as soluções de equilíbrio, ou seja, quando .
Como
Precisamos que
E isso acontece quando
Ou
Seno é igual a zero em dois pontos!!
Então essas são as soluções de equilíbrio.