- Mostre que a área das superfícies de uma zona de uma esfera que está entre dois planos paralelos é , onde é o raio da esfera e , a distância entre os planos. (Observe que depende apenas da distância entre os planos e não de sua localização, desde que ambos os planos interceptem a esfera.)
- Mostra que a área de superfície de uma zona de um cilindro com raio e altura é a mesma que a área de superfície da zona de uma esfera no item (a).
Passo 1
A equação da circunferência centrada na origem do plano é dada por .
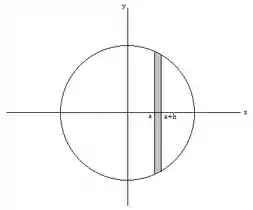
Vamos isolar o nessa equação e rotacionar ao redor de eixo com para gerar uma esfera.
A área da superfície pode ser escrita da seguinte maneira:
onde . Vamos descobrir quanto vale a primeira derivada da função:
Calculando a integral temos:
Passo 2
Para a letra (b), vamos rotacionar com ao redor do eixo para gerar a zona de um cilindro. Assim,
A área da superfície pode ser escrita da seguinte maneira:
onde . Vamos descobrir quanto vale a primeira derivada da função:
Calculando a integral, temos:
Resposta
Ei, a resposta está no passo a passo :)