Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 27
Mostre que a curva com equações paramétricas
está no cone , e use esse fato para esboçar a curva.
Passo 1
Eaee, tudo tranquilo?? Bom... o enunciado nos deu as seguintes equações paramétricas que descrevem uma curva:
O enunciado ainda nos disse que essa curva está dentro de um cone com equação:
Com isso, queremos esboçar a nossa curva.
Mas como fazemos isso???
Bom, pessoal... Para provar que a curva está de fato no cone, vamos tentar chegar na equação do cone a partir das equações paramétricas da curva.
Ou seja, vamos substituir duas equações paramétricas na equação do cone e vamos verificar se bateu o resultado!! Se bater, então está provado!! Aí é só a gente plotar depois 😉
Passo 2
Vamos pegar da equação do cone e vamos pegar as equações paramétricas e para substituir:
Colocando em evidência:
Sabemos de uma identidade trigonométrica que , portanto:
Então, como queríamos, chegamos na equação do cone substituindo :
Passo 3
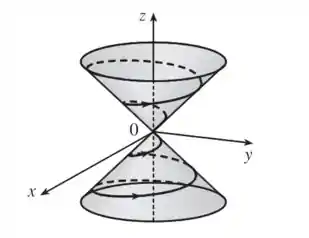
Show! Pela equação do cone, sabemos que a curva está contida num cone circular cujo eixo é o eixo .
E olhando pra equação paramétrica , acabamos de concluir que essa curva deve ser uma espiral, olha só:
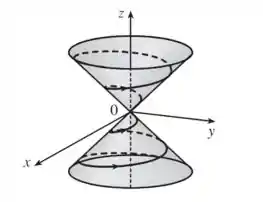
Resposta
