Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.1 - Ex. 23
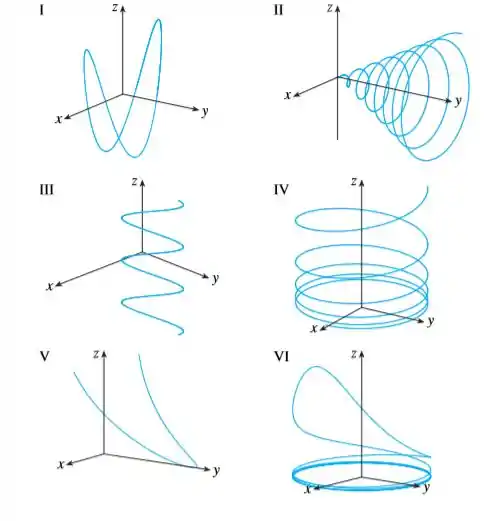
Faça uma correspondência entre as equações paramétricas e os gráficos (identificados com números de I-VI). Justifique sua escolha.
Passo 1
Fala galerinha!
A questão nos dá 3 funções de de modo que precisamos identificar qual das figuras representa uma função .
Para que consigamos identificar isso, precisamos avaliar como essa função se comporta nos planos .
Para isso, basta escrevermos a relação entre , e , dois a dois separadamente.
Encontrando o comportamento nos planos, podemos comparar com os gráficos para ver qual deles melhor representa a função .
Passo 2
A relação entre é dada por
Desse modo, o comportamento de nossa função no plano é o de uma parábola
A relação entre é dada por
Desse modo, o comportamento de nossa função no plano é o de uma hipérbole
A relação entre é dada por
Logo, o comportamento no plano também é o de uma hipérbole.
Passo 3
Sabendo o comportamento da função em todos os planos, precisamos comparar nossos resultados com os gráficos.
Dentre os gráficos, aquele que melhor se encaixa com o que descrevemos é o V por conta de seu comportamento nos planos ser igual ao esperado.
Resposta
O gráfico deve ser o V.