Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 50
Demonstre a Propriedade 5 dos vetores algebricamente para . Use então a semelhança de triângulos para fazer uma demonstração geométrica
Passo 1
Queremos mostrar algebricamente que
Então vamos dizer que e é um número qualquer.
Para mostrar o que queremos, podemos pensar na estratégia de desenvolver um dos lados da equação, depois o outro e no fim concluir que as duas respostas são iguais.
Começaremos fazendo
Beleza! Agora fazemos
Assim, conseguimos mostrar que
Passo 2
Agora vamos demonstrar a mesma coisa, só que de forma geométrica.
Para isso, pegamos um triângulo com um lado igual ao vetor e outro lado igual ao vetor , logo, o terceiro lado será a soma .
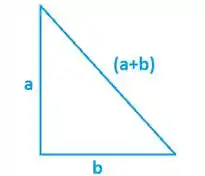
Se multiplicarmos os lados e por uma constante , notamos que a soma vetorial deve ser multiplicada pela mesma constante para completar o triângulo:
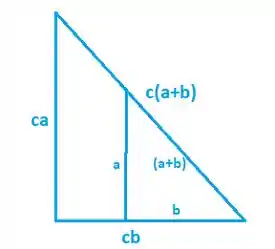
Assim, concluímos que
Resposta
Ei, a resposta está no passo a passo :)