Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 77
Mostre que a curva tem três pontos de inflexão e todos ficam sobre uma mesma reta.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui iremos provar, que a função dada possui 3 pontos de inflexão e que os 3 pontos ficam sobre a mesma reta.
Um ponto P na curva é chamado ponto de inflexão se f é contínua no ponto e a curva mudar de côncava para cima para côncava para baixo ou vice-versa em P.
Passo 2
Para achar o ponto de inflexão devemos achar a segunda e igualar a :
Vamos usar a regra da derivada da divisão, do polinômio e da constante:
Passo 3
Vamos derivar:
Passo 4
Vamos agora achar a segunda derivada:
Temos que:
e
O que nos dá:
e
Podemos confirmar que são pontos de inflexão testando os intervalos entre os zeros:
Intervalos adjacentes têm sinais diferentes, portanto, são pontos de inflexão.
Passo 5
Vamos provar agora que eles ficam na mesma reta, para isso podemos provar que a inclinação é igual a :
Vamos dizer então que , e
Vamos achar , e :
Passo 6
Substituindo de volta:
Então terminamos aqui nossa resolução.
Abaixo você pode ver os pontos
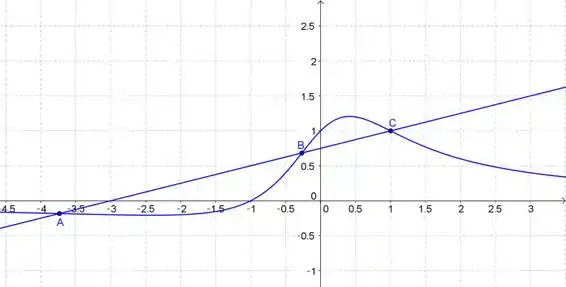
Resposta
Ver o desenvolvimento.