Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.3 - Ex. 2j
Esboce o gráfico de cada uma das funções do exercício anterior.
j)
Passo 1
Galera, vamos esboçar o gráfico de acordo com o estudo da função que fizemos no exercício anterior:
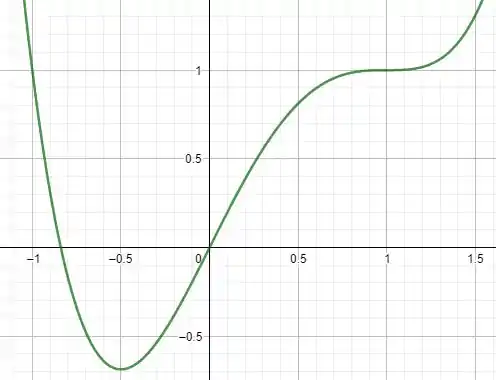
Note que o gráfico tem concavidade para cima em e e concavidade para baixo em , com pontos de inflexão em e .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Suponha que todas as funções sejam duas vezes deriváveis e que as segundas derivadas nunca sejam nulas.Se f e g forem funções positivas, crescentes e côncavas para cima em I , mostre que a função prod
Demonstre que se c , f ( c ) for um ponto de inflexão do gráfico de f e f ' ' existir em um intervalo aberto contendo c , então f ' ' c = 0 . [Sugestão: Aplique o Teste da Primeira Derivda e o Teorema
Mostre que se f x = x 4 , então f ' ' 0 = 0 , mas 0,0 não é uma ponto de inflexão do gráfico de f .
Mostre que a função g x = x x tem um ponto de inflexão em 0,0 , mas g ' ' ( 0 ) não existe.
Mostre que uma função cúbica (um polinômio de terceiro grau) tem sempre exatamente um ponto de inflexão. Se seu gráfico possui três intersecções com o eixo x , x ₁ ₁, x ₂ ₂ e x ₃ ₃, mostre que a coord