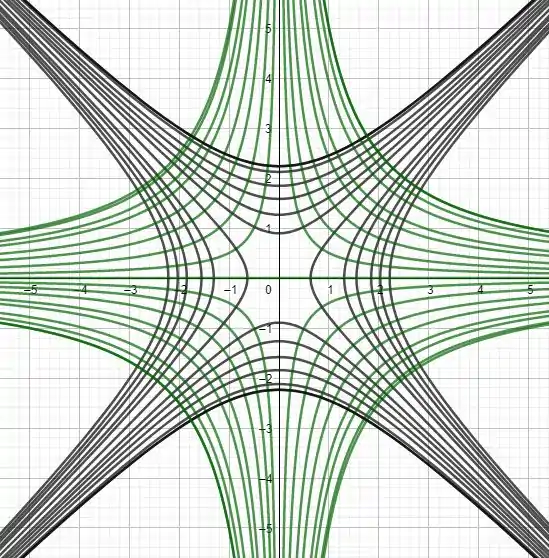
Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.

Primeiro, a gente vê qual a derivada da curva do enunciado. Pra isso, a gente deriva a equação dos dois lados:

Agora a gente quer que essa desapareça da face da Terra, mas é só olhar pra equação original e isolar o , jogando ele de volta na nossa derivada, confira:

Show! Já sabemos a derivada da curva do enunciado, agora como a gente vai relacionar isso com a derivada da trajetória ortogonal?

Bom, se as curvas formam , então suas retas tangentes também. Como a inclinação das retas é justamente a derivada, podemos aplicar aquela regrinha pra retas perpendiculares: trocar o sinal e inverter a fração da inclinação (ou derivada):

Tendo a derivada da trajetória ortogonal em termos de e (passo anterior), temos também uma equação diferencial separável que descreve essa curva. Então, se a gente resolvê-la, chegamos onde queremos, que é encontrar a equação da trajetória ortogonal. Vem comigo!

Prontinho! Chegamos à nossa tão sonhada resposta! Essa é a equação que descreve as trajetórias ortogonais, que tem cara de ser uma família de hipérboles. Agora só falta fazer um desenho bem da hora pra você ver como as duas famílias de curvas realmente são ortogonais!