Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 30
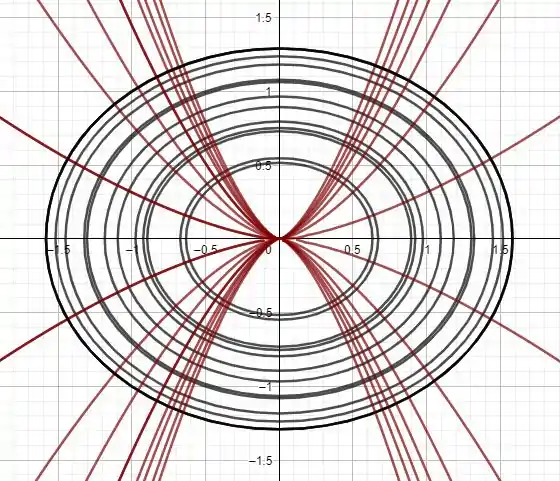
Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
Passo 1
Oi pessoal! Nessa questão a gente precisa encontrar as trajetórias ortogonais da curva descrita pela equação do enunciado, ou seja, vamos achar qual a equação da família de curvas que formam com a curva do enunciado, em cada ponto.
E se estamos falando de ângulo, também estamos falando de inclinação, de derivada. Ou seja, existe uma relação entre as derivadas dessas curvas para que elas formem , é isso que a gente vai explorar nesse exercício.
Passo 2
Então, primeiro, vamos descobrir qual a derivada da curva do enunciado. Pra isso, a gente deriva a equação dos dois lados, lembrando de usar a regra da cadeia:
O ideal aqui é fazer esse sumir, mas como? Olha a equação original, a gente pode extrair esse de lá:
Agora é só jogar ele de volta na derivada:
Passo 3
Agora que sabemos a derivada da curva do enunciado, qual relação a gente vai usar pra encontrar a derivada da trajetória ortogonal? Podemos usar aquela regrinha de que duas retas formam se a inclinação de uma é oposto e inverso da inclinação da outra. Ou seja, pra achar a derivada da trajetória ortogonal, é só trocar o sinal e inverter a fração da derivada da curva do enunciado, beleza galera?
Passo 4
Mas olha que belezura, ao encontrar a derivada, também obtemos uma equação diferencial separável correspondente à curva que desejamos conhecer. Bora resolver essa equação?
Chegamos onde queríamos! Encontramos a equação das trajetórias ortogonais, que parece ser uma família de elipses. Agora vamos comparar as duas famílias de curvas num desenho, pra você ver como faz sentido falar em “ortogonal” aqui.
