Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.4 - Ex. 12
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas.
Passo 1
Ao esboçar curvas polares, lembre-se de que é útil levar em conta a simetria, para isso, temos três regras:
- Se uma equação polar não mudar quando for trocado por , a curva será simétrica em relação ao eixo .
- Se a equação não mudar quando for trocado por , ou quando for trocado por , a curva será simétrica em relação à origem.
- Se a equação não mudar quando for trocado por , a curva será simétrica em relação à reta vertical (eixo ).
No enunciado temos:
Então, a nossa curva é simétrica em relação ao eixo , porque sabemos que:
A curva também é simétrica em relação à origem porque:
Logo, juntas, essas duas simetrias implicam a simetria em relação ao eixo .
Passo 2
Inserindo a equação no programa computacional WolframAlpha, conseguimos obter o seguinte gráfico:
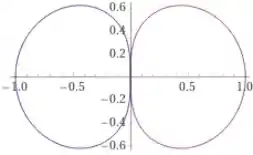
Resposta
Resposta no Passo.
Exercícios de Livros Relacionados
Trace a curva x = y - 3 y 3 + y 5
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de θ em coordenadas cartesianas. r = - 2 sen θ
18. Trace a cônica r = 4 / ( 5 + 6 cos θ ) e sua diretriz. Também trace a curva obtida pela rotação dessa cônica ao redor de seu foco por um ângulo π / 3 .
A ) Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumentaB ) Elimine os parâmetros para encontrar uma equação
A ) Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumentaB ) Elimine os parâmetros para encontrar uma equação