Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 7
Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas da grade que têm constante e quais têm constante.
Passo 1
Galera, para identificarmos a superfície, a melhor maneira é analisar a equação não parametrizada. Olhando para , podemos dizer que
Plotando em uma calculadora gráfica 3D, a superfície parametrizada é:
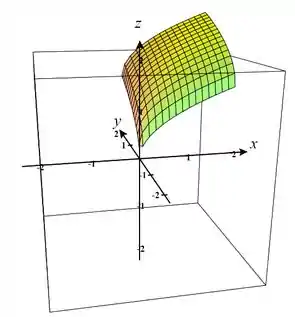
Passo 2
Vamos fazer com que seja constante. Assim, é uma constante, então as curvas correspondentes são as paralelas ao plano . Se fizermos constante, é uma constante, então as curvas correspondentes são as paralelas ao plano .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre as representações paramétricas das superfícies:A parte da esfera x 2 + y 2 + z 2 = 36 que está entre os planos z = 0 e z = 3 3 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A parte da superfície z = l
Encontre as equações paramétricas da superfície obtida pela rotação da curva x = 1 y , y ≥ 1 ao redor do eixo y e use-as para traçar o gráfico da superfície.
Encontre as equações paramétricas da superfície obtida pela rotação da curva y = 1 1 + x 2 , - 2 ≤ x ≤ 2 ao redor do eixo x e use-as para traçar o gráfico da superfície.
Encontre a área da superfície.Parte da superfície z = 4 - 2 x 2 + y que está acima do triângulo com vértices 0,0 ,( 1,0 ) e ( 1,1 ) .