Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 59

Seja

f x = x 3 + 2 x 4 + 1

(a) Gere o gráfico de y   =   f ( x ) e use-o para fazer estimativas das coordenadas dos extremos absolutos.

(b) Use um CAS para resolver a equação f ' ( x )   =   0 e, então, para fazer aproximações mais precisas das coordenadas de (a).

Passo 1

(a) O que a gente tem que fazer aqui é esboçar esse gráfico, e estimar por ele o ponto onde a função atinge o maior valor (máximo absoluto) e onde ela atinge o menor valor (mínimo absoluto).

Vamos usar a calculadora CAS do Geogebra (dá para acessar pelo navegador) para fazer o gráfico. Fica assim:

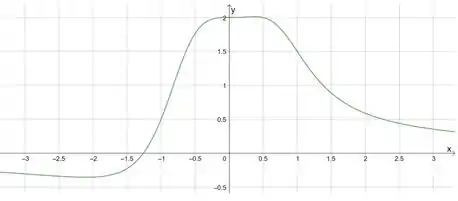
Por ele, vemos que o valor mais alto que a função assume, o máximo absoluto, está um pouco antes de x = 0,5 . Podemos estimar que está no ponto:

  x ≈ 0,4 ;         y ≈ 2,0 1  

E o valor mais baixo está perto de x = - 2 . Aí a gente pode estimar que o mínimo absoluto está em:

x ≈ - 2,1 ;         y ≈ - 0,3

Passo 2

(b) Agora a gente precisa confirmar se nossas estimativas estão fazendo sentido. Como? Vendo se a nossa função do enunciado tem pontos críticos próximos a esses que a gente estimou.

Vamos usar a calculadora CAS do Geogebra de novo para resolver a equação f ' x = 0 . Fica assim:

Olha só! Os pontos críticos estão bem próximos mesmo dos que a gente estimou! Então a gente vai dizer que o máximo absoluto está no ponto perto de x ≈ 0,4 , que é:

x = 0,372591 ;     y = f 0,37259 1 = 2,012931

E o mínimo absoluto é o ponto perto de x ≈ - 2,1 . Mais precisamente, ele está em:

x = - 2,111985 ;       y = f - 2,111985 = - 0,352941  

Resposta

(a) Máximo: x ≈ 0,4 ;         y ≈ 2,01 .

Mínimo: x ≈ - 2,1 ;         y ≈ - 0,3

(b) Máximo: x = 0,372591 ;     y = 2,012931

Mínimo: x = - 2,111985 ;       y = - 0,352941

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motorista de caminhão autônomo cobra de um cliente $ 15 por hora dirigida, acrescido do custo do combustível. Dirigindo a uma velocidade de v quilômetros por hora, o caminhão consegue fazer 10 - 0,
Em um certo processo de fabricação química, o peso diário y de produção defeituosa depende do peso x de toda a produção, de acordo com a fórmula empírica: y = 0,01 x + 0,00003 x 2 Onde x e y estão em
51-60 Dê um gráfico de polinômio e identifique as coordenadas dos cortes com os eixos, dos pontos estacionários e dos pontos de inflexão. Confira as respostas com um recurso gráfico.58- p x = 4 x 3 -
Mostre que dentre todos os retângulos com área A , o quadrado tem o perímetro mínimo.
Use o Método de Newton para aproximar o mínimo absoluto de f x = 1 4 x 4 + x 2 - 5 x .