Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 50
Uma mulher em um ponto na praia de um lago circular com raio de quer chegar no ponto diametralmente oposto a do outro lado do lago no menor tempo possível. Ela pode andar a uma taxa de e remar um bote a . Como deve proceder?
Passo 1
Opa, bora pra mais uma questão?! Temos um desafio dessa vez!
O enunciado fala de um lago com a forma de um círculo com um raio de . Tem uma mulher no ponto e ela quer chegar ao ponto que fica a um diâmetro de distância. Ela pode ir pela água remando com a velocidade de e andar a uma velocidade de .
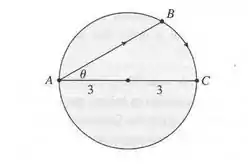
Temos que descobrir qual percurso que leva o menor tempo! Vamos olhar o desenho que o enunciado nos fornece:
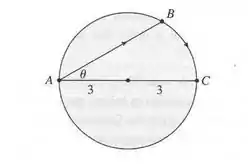
Nesse desenho ai de cima temos um percurso genérico, de modo que a mulher nadaria a distância e andaria uma distância . Podemos calcular o tempo fazendo:
Onde é o tempo, é a distância total e é a velocidade. Então teremos:
Temos que calcular mínimo, então vamos precisar desenvolver a função acima e deriva-la em relação ao tempo! Vamos colocar a mão na massa?
Passo 2
Ligando os pontos da figura dada e utilizando as propriedades da geometria, a gente pode formar uma figura assim:
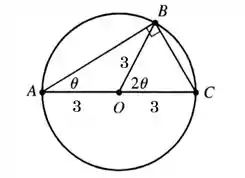
Como na figura se forma um triângulo isósceles com dois lados medindo , o ângulo também mede . O ângulo mede , então o ângulo mede:
Podemos dizer que:
Lembrando que representa a distância que a mulher irá remar. Já a distância que ela terá de andar, é representada pelo arco , que vale:
Então podemos então escrever:
Passo 3
Agora vamos calcular :
Calculando sua raiz:
Testando nos seus pontos extremos e em , temos:
O valor mínimo ocorre quando isso quer dizer que a mulher deve andar todo o caminho.
Valeu, galera! Até a próxima! 😉