Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 47

Um avião voando a uma velocidade constante de 300 km/h passa sobre uma estação de radar no solo a uma altitude de 1 km e subindo em um ângulo de 30 ° . A que taxa está crescendo a distância do avião em relação à estação de radar 1 minuto mais tarde?

Passo 1

O enunciado diz que um avião voando a uma velocidade constante de 300 km/h e passa sobre uma estação de radar no solo a uma altitude de 1 km e subindo em um ângulo de 30 ° .

E pede pra a gente calcular a que taxa de crescimento da distância do avião em relação à estação de radar 1 minuto depois.

Para melhor noção do que acontece, vamos ilustrar a situação, nomeando a distância do avião ao radar de y e x a distância do avião até o ponto em que passou quando estava exatamente em cima do radar:

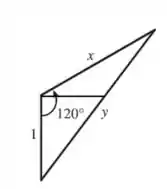
Temos aqui:

d x d t = 300   k m / h

E queremos: d y d t

Podemos escrever a relação entre x e y utilizando a lei dos cossenos:

y 2 = x 2 + 1 2 - 2 × 1 × x × cos ⁡ 120 °

y 2 = x 2 + x + 1

Passo 2

Derivando em função do tempo t em horas temos:

2 y d y d t = 2 x d x d t + d x d t

d y d t = d x d t ( 2 x + 1 ) 2 y

d y d t = d x d t ( 2 x + 1 ) 2 x 2 + x + 1

Após um minuto, o valor de x é:

x = 300   k m h o r a × 1 m i n u t o = 300   k m h o r a × 1 60 h o r a = 5   k m

Passo 3

Então:

d y d t = d x d t ( 2 x + 1 ) 2 y

d y d t = 300 2 5 + 1 2 5 2 + 5 + 1 = 1650 31 ≈ 296,35   k m / h

Logo, a distância do avião ao radar cresce com uma velocidade de 296,35   k m / h .

Resposta

A distância do avião ao radar cresce com uma velocidade de 296,35   k m / h .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

47. Às 8 da manhã, um navio que viaja para o norte com uma velocidade de 24 nós (milhas náuticas por hora) está em um ponto P. Às 10h, um segundo navio que viaja para o leste com uma velocidade de 32
18) Uma quadra de basebol é um quadrado de 90 pés. Um batedor atinge a bola e corre em direção à primeira base com uma velocidade de 24 pés/s.(a) A que taxa descreve sua distância da segunda base quan
Duas carretas, A e B , estão conectadas por uma corda de 12m que passa por uma polia P (veja a figura). O ponto Q no chão está 4m diretamente abaixo de P e entre as carretas. A carreta A está sendo pu
48. A produção diária de uma dada fábrica é de f ( x ) unidades quando o capital investido for de x milhares de uma unidade monetária $ e f x = 200 2 x + 1 . Se a capitalização corrente de $ 760.000 ,
49. Um avião está voando paralelamente ao chão, a uma altitude de 2Km e com uma velocidade escalar de 4 ½ km/min. Se em dado instante o avisão passar exatamente sobre a Estátua da Liberdade, qual será