Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 4.2 - Ex. 41b
Nesse problema, indicamos um modo de mostrar que, se r = r1 é uma raiz de multiplicidade s do polinômio característico Z(r), então e^r1t, te^r1t, . . . t^(s—1)e^r1t são soluções da Eq. (1). Esse problema estende para equações de ordem n o método para equações de segunda ordem dado no Problema 22 da Seção 3.4. Começamos da Eq. (2) no texto
e diferenciamos repetidas vezes em relação a r, fazendo r = r1 depois de cada diferenciação.
Diferenciando a Eq. (i) diversas vezes em relação a r, mostre que
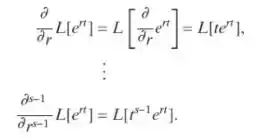
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a solução da nossa equação. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser considerar a equação dada no nosso enunciado
Passo 3
Pronto!! Agora é só substituir os valores e achar a solução!!
Se fizermos a parcial de cada lado, teremos: