Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 27
Neste exercício, consideramos a família de funções , onde é um inteiro positivo.
a) Faça os gráficos das funções , e , na mesma tela usando a janela retangular por .
b) Faça os gráficos das funções , e na mesma tela usando a janela retangular por .
c) Faça os gráficos das funções , , e na mesma tela usando a janela retangular por .
d) Que conclusões você pode tirar desses gráficos?
Passo 1
Fala aí! tudo certinho?
Nesse problema foram dadas uma família de funções do tipo e nosso objetivo é esboçar o gráfico de cada uma das função em uma janela que é dada em cada família.
Entendeu alguma coisa??
Sabemos que o gráfico da função é dado por
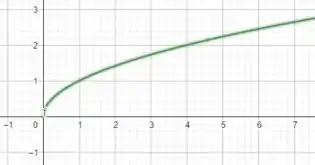
O valor de em influencia na acentuação do gráfico, ou seja, quanto maior , mais horizontal e mais brusco será subida.
Nessa família de funções, tem duas coisas que sempre acontecem... o gráfico sempre passa em e sempre passa pelo ponto . Além disso, se for par, a função será definida apenas em , mas se for impar, a função é definida em todos os reais.
A janela que é mencionada no problema, nada mais é que o intervalo de e que estamos interessados.
Veja só!
Passo 2
No item (a) devemos esboçar o gráficos das funções , e na janela por :
A primeira função é exatamente a função que já sabemos esboçar. Mas será um pouco mais brusco na subida até e depois será um pouco mais horizontal.
Já terá as mesmas características e ainda mais acentuada com relação a .
Tudo isso na janela e .
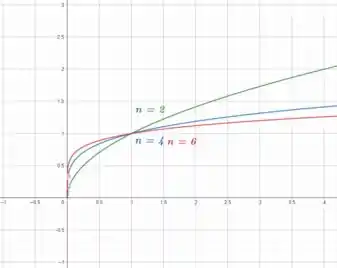
Tranquilo até aqui?
Passo 3
No item (b), devemos plotar as funções , e na janela por :
No caso de , seria como se fosse , então ele tambem faz parte da mesma família...
Porem, sabemos que é uma reta que como vimos no passo 1, se faz parte dessa família, passa por e .
Em e em vamos ter as mesmas características que pontuamos no passo anterior, lembrando que quanto maior , mais forte serão essas características.
A diferença é que agora, como são ímpares, a função está definida tanto para positivo quento para negativo.
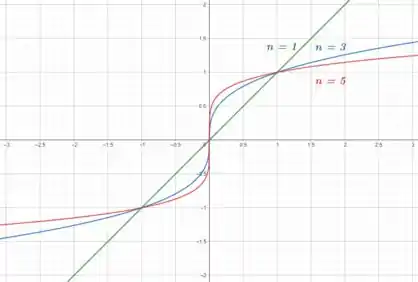
Show?
Passo 4
No item c) queremos esboçar os gráficos das funções , , e na janela retangular por .
Já esboçamos todas essas funções anteriormente, então é só copiar para a nova janela...
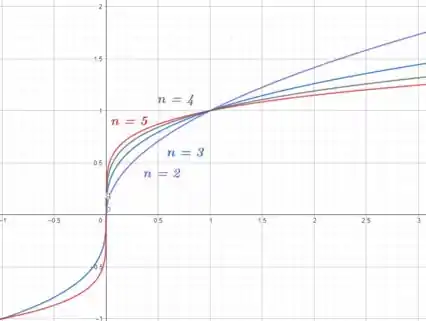
Bacana, não é?
Passo 5
Por fim, temos que concluir o que foi possivel tirar dos gráficos da família , para .
O que podemos concluir são que essa família de funções sequem características interessantes...
Vemos que para par, apenas a parte é definida, enquanto para ímpar a parte negativa do eixo pode ser definida.
Além disso, a função cresce mais para grande quando é menor e sempre passa pelos pontos e
E aí! o que achou? Responde Aí!
Resposta
Esboço de gráfico.