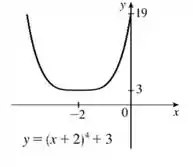
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.
Passo 1
E aí, preparado para resolver mais essa questão sobre transformação de gráficos e funções? Bora lá!
Bom, essa questão pede pra gente desenhar o gráfico da função
sem fazer isso ponto a ponto.
Isso é, usaremos uma das funções básicas que estão na seção 1.2 do livro e aplicaremos as transformações necessárias para transformá-la nessa daí. Isso vai ajudar a gente a desenhar esse gráfico de maneira mais rápida e fácil.
Show de bola. Vamos ver quais são as características dessa função e qual a função básica que mais se parece com ela para fazer as mudanças adquadas. Vem que te ajudo com isso.
Passo 2
Bom, perceba que nossa função é do tipo
Essa função tem uma potência de expoente onde a variável está. Isso nos lembra a função básica do tipo:
Então, começamos pegando o gráfico de na seção do Stewart, que vai ser esse aqui:
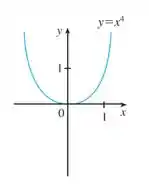
A diferença é que temos na basse da potência. Além disso, temos a adição de 3 unidades na função. Isso que dizer que podemos usar essa função como nossa base, mas precisaremos de algumas altereções em seu gráfico.
Passo 3
Agora vamos entender o que devemos fazer para encontrar o gráfico da função .
Vamos fazer aqui uma pequena alteração, chamando .
Com isso a função que era:
Se torna
Agora vou te dar uma super dica. Sempre que isso puder ser feito, significa que está acontecendo um deslocamento horizontal da função.
Isso porque se
Teremos:
Ou seja, para conseguir o gráfico de , só precisamos deslocar a função para a esquerda em unidades.
Uma soma o subtração junto ao sempre provoca um deslocamento na horizontal. E nosso gráfico será:
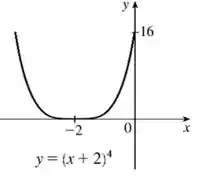
Passo 4
Além disso, observe que a troca que fizemos ainda possui a adição de unidades no gráfico anterior.
Isso fará com que nossa função seja deslocada em 3 unidade na vertical para cima.
Percebe que o ele não ta somando colado no como o o , por isso o efeito vai ser diferente! Dá uma olhada:
Assim, o gráfico resultante já vai ser a nossa resposta, dá só uma olhada:
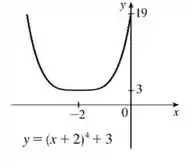
Pronto, terminamos! Esse último gráfico é a nossa resposta!
Resposta
O gráfico de é: