Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 28
Neste exercício, consideramos a família de funções , onde é um inteiro positivo.
a) Faça o gráfico das funções e , na mesma tela usando a janela retangular por .
b) Faça o gráfico das funções e na mesma tela usando a janela retangular dada na parte (a).
c) Faça o gráfico de todas as funções das partes (a) e (b) na mesma tela, usando a janela retangular por .
d) Que conclusões você pode tirar desses gráficos?
Passo 1
Fala aí, tud certinho com você?
Bom, essa questão pede pra gente considerar a família de funções
Com sendo um inteiro positivo, para obter algumas conclusões sobre seus gráficos.
E para isso, teremos que desenvolver 4 diferentes itens, sendo eles:
a) Fazer o gráfico das funções e , na mesma tela usando a janela retangular por .
b) Fazer o gráfico das funções e na mesma tela usando a janela retangular dada na parte (a).
c) Fazer o gráfico de todas as funções das partes (a) e (b) na mesma tela, usando a janela retangular por .
d) Que conclusões você pode tirar desses gráficos?
Sendo assim, precisaremos fazer uma coisa de cada vez. Vem comigo que te ajudo passo a passo.
Passo 2
No item (a) devemos esboçar o gráfico das funções
e
na janela por .
Mas o que isso significa?
As janelas que estamos falando aqui são regiões retangulares delimitadas pelos intervalos de e .
Neste caso, temos por . Isso significa que a lagura da janela começa em e vai até , e a altura começa em e vai até .
Assim, nosso esboço será:
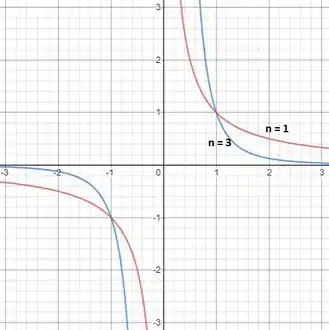
Perceba que as funções e estão em cores diferentes e indica o expoente de .
Assim, funções é a que está em vermelho e é a que está em azul.
Passo 3
No item (b), devemos plotar as funções com e na mesma janela do item (a). Então já conhecemos o intervalo. Assim, teremos:
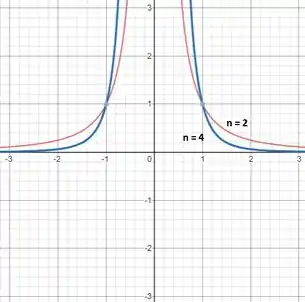
Passo 4
Por fim, no item (c), temos que plotar todas as funções na janela por .
Então mudando a janela, teremos:
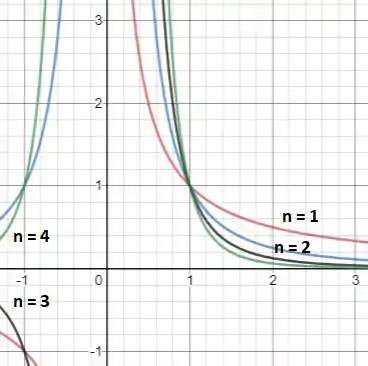
Passo 5
Agora vamos observar tudo que fizemos até aqui pra responder item d).
Perceba que quando é par, a função
é uma função par. Lembrando que a função par é definida por:
Isso pode ser observado devida a sua simetria em relação ao eixo .
Enquanto para ímpar, a função será uma função ímpar. O que pode ser observado nos gráficos quando a função é rebatida em relação a origem. E sua definição é:
Além disso, vemos que a janela reduzida do item (c) não cobre bem os gráficos em toda sua extensão!
Resposta
a), b) e c) Esboço de gráfico.
d) Quando é par, a função
é uma função par.
Enquanto para ímpar, a função será uma função ímpar.
Além disso, vemos que a janela reduzida do item (c) não cobre bem os gráficos em toda sua extensão!