Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.1 - Ex. 25a
Usando um tamanho de passo e o método de Euler, mas mantendo apenas três dígitos ao longo dos cálculos, determine valores aproximados para a solução em para cada um dos problemas de valor inicial a seguir.
A -
Compare os resultados com os obtidos no Exemplo 1 e nos Problemas 1 e 3. As pequenas diferenças entre alguns dos resultados arredondados para três dígitos e os resultados atuais são causadas pelo erro de arredondamento. O erro de arredondamento tornar-se-ia importante se os cálculos exigissem muitos passos.
Passo 1
Bem, essa questão teremos que criar um programinha que nos dê a solução dessa EDO:
Para isso, podemos usar esse modelinho aqui que o Boyce nos deu no capítulo dele:
SIM! Vamos ter que usar programação, assim como em todas as questões desse capítulo rsrsrs. Aqui eu vou utilizar a língua C++, ok? Como o problema não específica você pode utilizar a língua que você se sente confortável .
Passo 2
O Script na linguagem C++ para resolver esse problema seguindo aquele modelinho ali em cima (que nós chamamos de lógica) ficou assim:
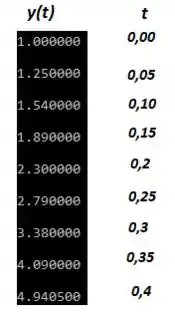
Você pode copiar esse código em algum compilador na internet de C++. Quando você o executa, ele vai te dar os seguintes valores:
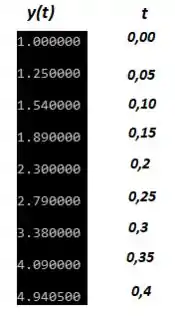
Os comparando com os valores obtidos no exemplo 1 deste capítulo...
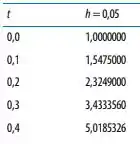
Percebe-se que o fato de termos usado três casas decimais fixas, alterou-se pouco os nossos resultados, principalmente porquê estamos falando de um pequeno, saca?
Resposta
